- #1
Number2Pencil
- 208
- 1
Homework Statement
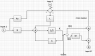
I'm having to figure out if a system is asymptotically stable, stable, or unstable. I am given the system block diagram. However, each constant block is actually a matrix. Also, there is an integral block thrown in there...
Homework Equations
The Attempt at a Solution
In a regular, non-matrix system, I would reduce the block diagram until I arrive at the the system's equivalent transfer function in a canonical form, and then analyze the values of the roots to determine the system stability. The integral block would be a 1/s block...I believe
Since this is a matrix system however, I'm not exactly sure what to do. Should I still reduce the block diagram as if it was not matrix-constants and then perform some kind of analysis on the Matrix-laden system transfer function...or maybe start off by breaking up all the matrix math into individual element formulas?
Not really sure what to do in this case...