Schwann
- 7
- 4
- TL;DR
- Does PSD computed from concatenated epochs of time series differ from PSD computed from averaged epochs of the same time series?
I have a question related to linearity of power spectral density calculation.
Suppose I have a time series, divided into some epochs. If I compute PSD by Welch's method with a time window equal to the length of an epoch and without any overlap, I obtain this result:
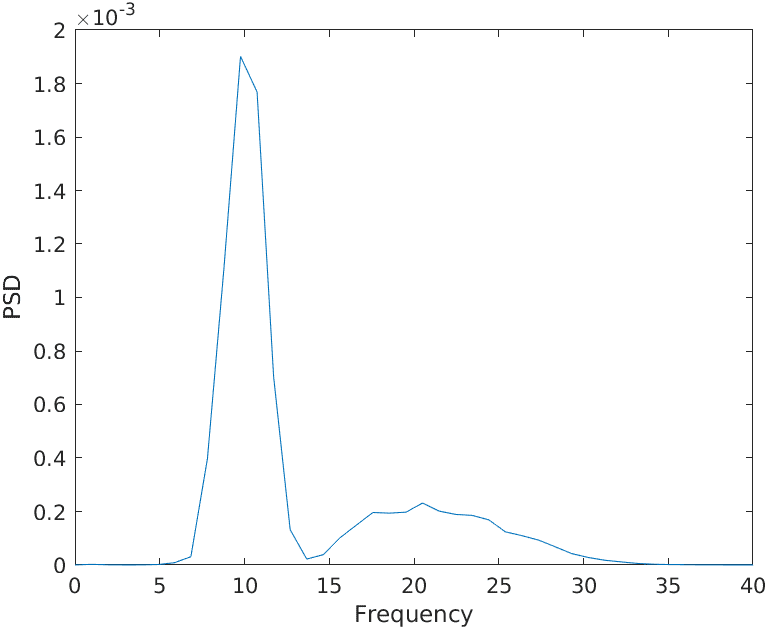
If I calculate the average of my time series over the epochs, obtain the averaged signal, the length of which is equal to the length of one epoch (obviously), and then compute PSD by the same method using this averaged signal, I get a slightly different result:
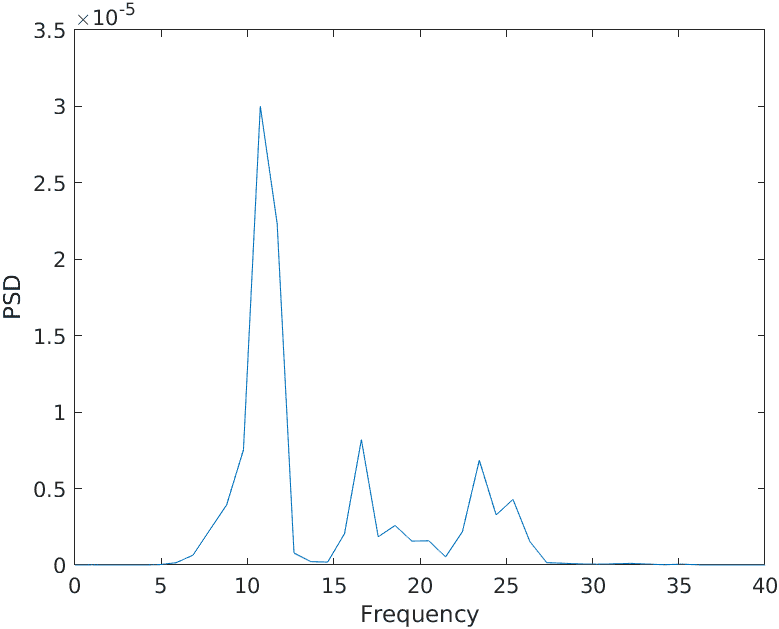
I thought that these two scenarios could not be different, as PSD from the concatenated epochs is presumably equal to PSD from averaged epochs (in my opinion). However, the results are different.
I am looking for analytical explanation of these discrepancies.
Thank you!
Suppose I have a time series, divided into some epochs. If I compute PSD by Welch's method with a time window equal to the length of an epoch and without any overlap, I obtain this result:
If I calculate the average of my time series over the epochs, obtain the averaged signal, the length of which is equal to the length of one epoch (obviously), and then compute PSD by the same method using this averaged signal, I get a slightly different result:
I thought that these two scenarios could not be different, as PSD from the concatenated epochs is presumably equal to PSD from averaged epochs (in my opinion). However, the results are different.
I am looking for analytical explanation of these discrepancies.
Thank you!
