Looking for Doppler Solution to Maxwell's Equations?

[tade]

I'm looking for an EM wave solution to Maxwell's equations that matches the Doppler diagram below.

That is, circular wavefronts that are not concentric due to the motion of the source.

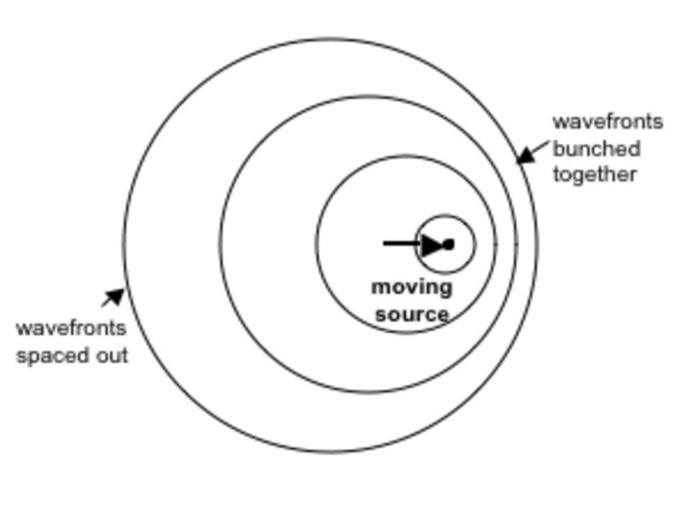
Does a solution that accurately matches the Doppler diagram exist?

 

[Dale]

The easiest way to get such a solution would be to take e.g. the dipole solution and Lorentz transform it to a different reference frame.

 

[tade]

The easiest way to get such a solution would be to take e.g. the dipole solution and Lorentz transform it to a different reference frame.

If so, it will preserve the wavefronts' circular shape right?

 

[Dale]

Yes, they will each be spherical, but centered on a different point. This is what causes the classical part of the Doppler shift.

 

[tade]

alright, thanks Dale. you're always a great help