Lowering an object without breaking the the rope

  • Thread starter Thread starter Kingyou123
  • Start date Start date
  • Tags Tags
    Rope
AI Thread Summary
To lower a 1000 N object using a cord with a breaking strength of only 800 N, the acceleration must be reduced so that the net force does not exceed the cord's limit. The weight of the object is calculated as 1000 N, which corresponds to a mass of approximately 102.04 kg. The attempt to find the acceleration resulted in a value of 7.84 m/s², which is incorrect as it does not account for the tension in the cord. A free body diagram should be drawn to visualize the forces acting on the object, which include weight and tension. The correct approach involves ensuring the sum of forces remains within the safe limits of the cord's breaking strength.
Kingyou123
Messages
98
Reaction score
0

Homework Statement


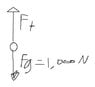
How could a 1000 N object be lowered from a roof using a cord whose breaking strength is only 800 N?

Homework Equations


∑F=ma

The Attempt at a Solution


By slowing down the acceleration to a point where the force down would be less than 800.
weight=m(g)
1000N=m(9.8)
102.04kg=m
∑F=ma
799.99=102.04kg(a)
7.84m/s^2=a
Would this be the right answer?
 
Last edited:
Physics news on Phys.org
This is not the correct answer. Be sure to draw a free body diagram of the object. How many forces act on the object as it is being lowered?
 
  • Like
Likes Kingyou123
TSny said:
This is not the correct answer. Be sure to draw a free body diagram of the object. How many forces act on the object as it is being lowered?
The two forces are weight and force tension. Where did I go wrong exactly?
 

Attachments

  • Snapshot.jpg
    Snapshot.jpg
    5.4 KB · Views: 369
Diagram looks good. When you set up ∑F = ma, the left side represents the vector sum of the two forces.
 
Last edited:
  • Like
Likes Kingyou123

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Monkey accelerating up and down a rope
Replies
38
Views
4K
Tension force of block and rope
Replies
25
Views
5K
Tension on a Massive Rope: How to Calculate Tension at Different Points
Replies
11
Views
3K
How Does Nick's Acceleration Change When His Friend Pulls the Rope?
Replies
6
Views
3K
Lowering a climber with the belay rope routed through a pulley at an angle
Replies
12
Views
2K
Elevator Problem: Determining Scale Reading for a Moving Object
Replies
5
Views
1K
Frequency and wavelength of a wave on a vertical rope
Replies
4
Views
4K
Understanding Sign Conventions in Elevator Tension Problems
Replies
6
Views
3K
Finding the Mass of a Hanging Rope (Wave Problem)
Replies
4
Views
2K
Why Does Tension Vary Along the Rope in a Hanging Superhero Scenario?
Replies
5
Views
7K

Hot Threads

Recent Insights

Back
Top