Magnet with negative charge in gaussian surface?

[marshmallow]

i would really appreciate if someone could help me out with this one. i m preparing for an exam and this question is a question from papers of previous years and its bugging me because it seems very specific in that i can't seem to find anything like it in textbooks.

what i m mainly stuck on is if a negative charge is spread over the magnet does this mean the direction of the magnetic field reverses from north to south to south to north?



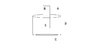
A bar magnet has been given a negative charge -Q, spread uniformly over the magnet.

the Gaussian cylinder shown at right with end caps A and C and a curved side B. the centre of cap A coincides with the centre of the bar magnet.

(a) is the total electric flux through the top end of the cap, A, positve, negative or zero?

(b) is the total electric flux through the entire gaussian surface, consisting of sides A,B, and C, positive, negative, or zero?

(c) is the total magnetic flux through the top end cap, A, positive, negative or zero?

(d) is the total magnetic flux through the entire gaussian surface, consisting of sides A, B, and C, positve, negative, or zero?

 

[cragar]

Well the total electric flux through that pill box will be the charge inside divided by the permittivity constant . So it should be half of negative Q divided by epsilon .
Magnetic field lines flow from north to south pole so i think the pill box will have a negative magnetic flux, because the field lines are flowing into the box and not out of it.
And of course if the pill box was around the whole magnet the magnetic flux would be zero because we have as much flowing out as we having flowing in .
I hope someone can check this .

 

[AJ Bentley]

This is an exercise in divergence of B and E. Divergence of E is equal to the charge inside (ignoring dimensionless constants). Whereas divergence of B is zero. (no magnetic 'charges' exist). So:-

a) The electric charge is distributed uniformly either side of the cap so the electric flux through it will be the same from each side therefore net flux = zero.

b) The entire Gaussian surface encloses a quantity of negative charge so the flux out of it will be negative.

c) This one is tricky. The flow of magnetic flux is from north to south outside the magnet but inside it, it must be from south to north (because the divergence of B is zero - the flux must flow in a complete loop). That means that the surface A intercepts all of the flux from south to north inside the magnet but only part of the flux on the outside. (because it isn't infinite - some flux goes round it). As to whether that is positive or negative flow depends on how you choose to call it.

d) Since the divergence of B is zero, there can be no net magnetic flux into or out of a Gaussian surface under any circumstances, so it's zero.