Magnetic field and wire current

Click For Summary

Homework Help Overview

The problem involves a long, straight wire suspended in a uniform magnetic field, where a current flowing through the wire experiences a magnetic force causing it to deflect at an angle. The objective is to determine the strength of the magnetic field based on the given parameters.

Discussion Character

  • Exploratory, Conceptual clarification, Problem interpretation

Approaches and Questions Raised

  • The original poster attempts to find the radius 'r' needed to apply a specific equation for the magnetic field. Some participants question the relevance of the equation initially cited and suggest considering the force on a current-carrying wire in a magnetic field.

Discussion Status

Participants are engaging in clarifying the appropriate equations to use for the problem. Guidance has been offered regarding the use of the force equation for a current-carrying wire, and the suggestion to draw a free body diagram has been made to help balance the forces involved.

Contextual Notes

The original poster has noted the given parameters but is struggling with the missing information regarding the radius 'r', which is necessary for their calculations.

dmsgo89
Messages
9
Reaction score
0

Homework Statement


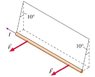
A long, straight wire with linear mass density of 45g/m is suspended by threads, as shown in the figure . There is a uniform magnetic field pointing vertically downward. A 7.0A current in the wire experiences a horizontal magnetic force that deflects it to an equilibrium angle of 10 degree. What is the strength of the magnetic field B?



Homework Equations



B=(U_o I) / (2 *3.14 * r)


The Attempt at a Solution



I have U_0 given, I given. but can't find r.

How can find r to get B?
 

Attachments

  • jfk_Figure_24_P59.jpg
    jfk_Figure_24_P59.jpg
    8.4 KB · Views: 758
Physics news on Phys.org
The equation that you have quoted gives the magnetic field produced by a very long wire. It is not relevant here. What equation do you know that gives the force on a current-carrying wire segment in a magnetic field?
 
F=ILB maybe?
 
That's the right equation.
The next step is to draw a free body diagram and balance the forces.
 

Similar threads

Calculating Magnetic Field at Point P for Perpendicular Current-Carrying Wires
  • · Replies 2 ·
Replies
2
Views
1K
Induced current and force on circular loop in varying magnetic field
  • · Replies 4 ·
Replies
4
Views
1K
Magnetic field pointing into a normal magnetized compass needle
  • · Replies 16 ·
Replies
16
Views
2K
Why is magnetic field B along a straight wire circular not radial?
  • · Replies 14 ·
Replies
14
Views
3K
Electromagnetism question -- Forces between two current carrying wires
  • · Replies 7 ·
Replies
7
Views
3K
Direction and magnitude of electric field produced by current change
  • · Replies 8 ·
Replies
8
Views
2K
EM fields and Current between 2 charged cylinders
  • · Replies 10 ·
Replies
10
Views
2K
Non-Uniform Magnetic Field Calculations
  • · Replies 9 ·
Replies
9
Views
2K
Surface current of superconducting sphere in magnetic field
  • · Replies 1 ·
Replies
1
Views
1K
Force between two halves of a current carrying hollow cylinder
  • · Replies 3 ·
Replies
3
Views
1K