Magnetic Field at Center of Loop

AI Thread Summary
The discussion focuses on calculating the magnetic field at the center of a loop, where the standard formula B = Mu_0*I/(2*R) was initially applied but yielded an incorrect result. Participants noted that the configuration includes both a loop and a straight wire, which complicates the calculation. It was suggested to use the principle of superposition to combine the magnetic fields from both the loop and the straight wire. The conversation highlights the importance of recognizing the unique shape of the cable in relation to the formula. Ultimately, the correct approach involves adding the magnetic fields from both components to find the total strength at the center.
tomizzo
Messages
113
Reaction score
2

Homework Statement



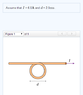
What is the strength of the magnetic field at the center of the loop in the figure?

See attachment

Homework Equations



B = Mu_0*I/(2*R)

The Attempt at a Solution



I plug in the information to this equation and get .00038 Tesla which is incorrect. Does the magnetic field due to a loop equation I listed above not apply to this problem?
 

Attachments

  • Capture.PNG
    Capture.PNG
    4.1 KB · Views: 654
Physics news on Phys.org
The loop is fine, but the cable is not just a simple loop...
 
mfb said:
The loop is fine, but the cable is not just a simple loop...

What is special about it?
 
Do you see the difference between the shape of the cable and a circle?
 
mfb said:
Do you see the difference between the shape of the cable and a circle?

There is some over lap. I thought it still fitted the formula above due to the fact that it is a coil with a single turn.
 
I spy with my little eye: a loop and a straight wire carrying a current!
 
BvU said:
I spy with my little eye: a loop and a straight wire carrying a current!

Using superposition, you will simply added the magnetic field due to the straight wire to the magnetic field due to the loop. Thank you!
 
Bravo! and: you're welcome.
 

Similar threads

Can the Magnetic Field Be Determined Using Biot-Savart Law Superposition?
Replies
2
Views
948
Magnetic energy density, self-inductance of coaxial cylindrical shells
Replies
10
Views
1K
Induced current and force on circular loop in varying magnetic field
Replies
4
Views
1K
Understanding Torque in a Magnetic Field with Loop
Replies
37
Views
4K
How to obtain correct negative sign in calculation of motional emf?
Replies
2
Views
902
Making sense of sequence of ideas in MIT OCW's 8.02 notes on Faraday
Replies
1
Views
1K
Why is a current ring approx a magnetic dipole from very far off?
Replies
7
Views
2K
Surface current of superconducting sphere in magnetic field
Replies
1
Views
829
Calculating magnetic field outside a solenoid
Replies
15
Views
1K
Why are the effects of a magnetized material neglected in this case?
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top