Magnetic field due to current in straight wire(Biot-Savarts)

[san203]

Hello.
The Magnetic Field lines are concentric circles for a Straight wire.Hence the points above and below point B should not contribute to the magnetic field at A.
So Why do we integrate the expression across the whole length of the wire to get magnetic field at point A?

 

[jtbell]

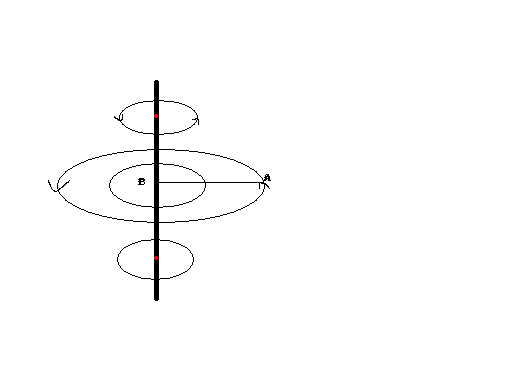
The Magnetic Field lines are concentric circles for a Straight wire.Hence the points above and below point B should not contribute to the magnetic field at A.

The "Hence" does not follow. The field at point A is the sum of contributions from all parts (infinitesimal segments of length $dl$) of the wire. For an infinitely long wire (which is of course only an idealization) we integrate $dl$ from $-\infty$ to $+\infty$. For a finitely long wire we integrate between some limits a and b.

 

[san203]

The "Hence" does not follow. The field at point A is the sum of contributions from all parts (infinitesimal segments of length $dl$) of the wire. For an infinitely long wire (which is of course only an idealization) we integrate $dl$ from $-\infty$ to $+\infty$. For a finitely long wire we integrate between some limits a and b.

So you mean that every dl part of the wire contributes to the net field. But isn't the magnetic field lines Concentric? How can they intersect?

 

[Jasso]

What would the field look like around an infinitely short current segment $dl$?

Would it still form concentric rings, or would it be different?

 

[dauto]

The magnetic lines don't intersect.

 

[Philip Wood]

Remember that a magnetic field line is a line whose direction at every point is the direction of the RESULTANT field at that point. Just because the circle is centred at one point on the wire doesn't mean that that point is responsible by itself for the field line.

 

[san203]

Remember that a magnetic field line is a line whose direction at every point is the direction of the RESULTANT field at that point. Just because the circle is centred at one point on the wire doesn't mean that that point is responsible by itself for the field line.

I seemed to have overlooked that part. Maybe i am not thorough with the basics.
So, i guess a small circuit element is able to exert magnetic field at every point in its plane and that magnetic field is perpendicular the plane?

 

[Philip Wood]

Yes. The only nitpick is that a straight line doesn't define a plane. There are an infinite number of planes which contain the element.