ks_wann
- 14
- 0
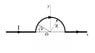
So, I've got a wire with a semicircle about the origin, my task is to find the magnetic field at M=(0,0,z).
I want to use Biot-Savart, so I find dl', r and r-hat. (r being the vector from the source point to field point)
\begin{equation}
r^{2}=R^{2}+z^{2}\\
\mathbf{r}=R\cos{\theta}\mathbf{\hat{i}}+R\sin{\theta}\mathbf{\hat{j}}+z\mathbf{\hat{k}}\\
d\mathbf{l^{\prime}}=Rd\theta \mathbf{\hat{\theta}}
\end{equation}
With these identified, I use biot-savart:
\begin{equation}
\mathbf{B}(\mathbf{r})=\frac{\mu_{0}I}{4\pi}\int\frac{d\mathbf{l^{ \prime}}\times\mathbf{\hat{r}}}{r^{2}}
\end{equation}
What troubles me is the cross product. I get
\begin{equation}
d\mathbf{l^{\prime}}\times\mathbf{\hat{r}}=\frac{R}{\sqrt{R^{2}+z^{2}}} \mathbf{\hat{\theta}}\times(R\cos\theta \mathbf{\hat{i}}+R\sin\theta \mathbf{\hat{j}}+z\mathbf{\hat{k}})
\end{equation},
and I'm not sure what to make of it as the unit vector would change all the way through the semicircle.
I want to use Biot-Savart, so I find dl', r and r-hat. (r being the vector from the source point to field point)
\begin{equation}
r^{2}=R^{2}+z^{2}\\
\mathbf{r}=R\cos{\theta}\mathbf{\hat{i}}+R\sin{\theta}\mathbf{\hat{j}}+z\mathbf{\hat{k}}\\
d\mathbf{l^{\prime}}=Rd\theta \mathbf{\hat{\theta}}
\end{equation}
With these identified, I use biot-savart:
\begin{equation}
\mathbf{B}(\mathbf{r})=\frac{\mu_{0}I}{4\pi}\int\frac{d\mathbf{l^{ \prime}}\times\mathbf{\hat{r}}}{r^{2}}
\end{equation}
What troubles me is the cross product. I get
\begin{equation}
d\mathbf{l^{\prime}}\times\mathbf{\hat{r}}=\frac{R}{\sqrt{R^{2}+z^{2}}} \mathbf{\hat{\theta}}\times(R\cos\theta \mathbf{\hat{i}}+R\sin\theta \mathbf{\hat{j}}+z\mathbf{\hat{k}})
\end{equation},
and I'm not sure what to make of it as the unit vector would change all the way through the semicircle.
Attachments
Last edited: