- #1
Nick89
- 555
- 0
This is not really a homework problem, just something that struck me as weird while revising for an exam...
Consider an infinitely long straigt wire with an also infinitely long hole cut out of it.
Then imagine cutting the wire in half, as in the following picture:
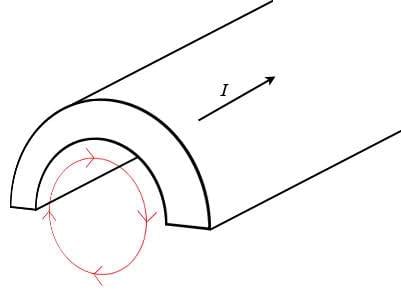
The 'wire' carries a current I along it's axis.
Now, according to Ampere's law for magnetic fields (see below) there should be no magnetic field inside the hole, right?
Why is this?
I can imagine it if the wire was not cut in half (just a wire with a hole in it) since than the field would cancel itself out (top side cancels out lower side, left side cancels out right side, and so on for every 'pair' of sides).
Now however, that is not the case... So how come there is still no magnetic field in the hole? I just can't imagine this, I think it's weird...
Am I not seeing something obvious maybe?
Ampere's law:
[tex]\oint \vec{B} \cdot \vec{dl} = \mu_0 I_{\text{enclosed}}[/tex]
Using Ampere's law as stated above, with the integral path shown in red in the picture, I find the enclosed current to be 0, resulting in a magnetic field B of also 0...
Is this right, or am I doing something horribly wrong?!
Homework Statement
Consider an infinitely long straigt wire with an also infinitely long hole cut out of it.
Then imagine cutting the wire in half, as in the following picture:
The 'wire' carries a current I along it's axis.
Now, according to Ampere's law for magnetic fields (see below) there should be no magnetic field inside the hole, right?
Why is this?
I can imagine it if the wire was not cut in half (just a wire with a hole in it) since than the field would cancel itself out (top side cancels out lower side, left side cancels out right side, and so on for every 'pair' of sides).
Now however, that is not the case... So how come there is still no magnetic field in the hole? I just can't imagine this, I think it's weird...
Am I not seeing something obvious maybe?
Homework Equations
Ampere's law:
[tex]\oint \vec{B} \cdot \vec{dl} = \mu_0 I_{\text{enclosed}}[/tex]
The Attempt at a Solution
Using Ampere's law as stated above, with the integral path shown in red in the picture, I find the enclosed current to be 0, resulting in a magnetic field B of also 0...
Is this right, or am I doing something horribly wrong?!