Magnetic Field of a long straight wire

[stunner5000pt]

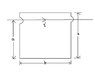
for the figure
a=12cm, b= 16cm
The current in a long straight wire is given by $i = (4.5 A/s^2)t^2 - (10A/s)t$. Find the emf in the square loop at t=3.0s
now i was wondering how one would go about caluclating hte B in the square loop.
Would i use the biot savart law or Ampere's law?
I have a feeling it is ampere's law so that
$$\oint B \bullet ds = \mu_{0} i$$
but then what is ds? The amperian loop in thsi case would be a cylinder that encompasses the whole square and more...
Please help on this
thank you for the help

 

[bigplanet401]

Skip Ampere and Biot-Savart, unless you've never derived the result for the magnetic field from an infinite straight wire before! Here's the result:
$$\begin{equation} \mathbf{B} = \frac{\mu_0 I(t)}{2\pi \rho} \hat{\phi} \, ; \end{equation}$$
$$\rho$$ is the radial coordinate (in cylindrical coordinates). Now take this result, and forget about Ampere's law. You need to compute the flux in the loop.
First notice that (1) is singular at $$\rho = 0$$. Second: we need to define an area element, since the total flux is written in terms of a surface integral. The area element
is $$d\rho \, dz \hat{\phi}$$, and so
$$\text{Flux } = \int \mathbf{B} \cdot d\mathbf{A} = +\int_0^b \int_\epsilon^{b-a} \frac{\mu_0 I(t)}{2\pi \rho} \, d\rho \, dz - \int_0^b \int_\epsilon^a \frac{\mu_0 I(t)}{2\pi \rho} \, d\rho \, dz\, .$$
We're taking care of the problem at zero by coming arbitrarily close to the wire, but never integrating across it. (Why is there a minus sign in the second integral?)
The epsilons should cancel, and your result should be dimensionally correct. Now that you have the flux, go ahead and differentiate the current with respect to time to get
$$\mathcal{E}$$.