CaneAA
- 13
- 0
Homework Statement
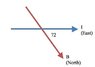
A high-voltage power lines carries a current of 110 A at a location where the Earth's magnetic field has a magnitude of .59 G and points to the north, 72 degrees below the horizontal. Find the direction and magnitude of the magnetic force exerted on a 250-m length of wire if the current in the wire flows (a) horizontally toward the east or (b) horizontally toward the south.
Homework Equations
F=ILBsintheta
The Attempt at a Solution
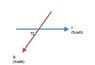
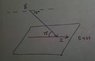
What confuses me about this problem is setting up the magnetic field "pointing north, 72 degrees below the horizontal." I've attached a sketch, I don't know if it is correct.
If it is then the F=(110)(250)(5.9*10^-5)sin72 = 1.54 N
And with the 2nd RHR I get that the force is pointing in the positive z direction.
For part B, I don't know how the sketch would change. The current is still "horizontal", but this time, the horizontal direction points the the south. Does the angle with the current stay the same?