Magnetohydrodynamics - Derivation of PDE

n0b1
Messages
2
Reaction score
0
Summary:: partial differential equation (PDE) to describe the potential distribution φ in the system

Hey, I need some help with the following question:

We have a stationary electrolyte, a magnetic field "B" and a Current density "j" (2D).

Derive the partial differential equation (PDE) to describe the potential distribution φ in the system by balancing the charges first.

1613333524623.png


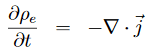
I don't know how to do anything?
1613333505396.png

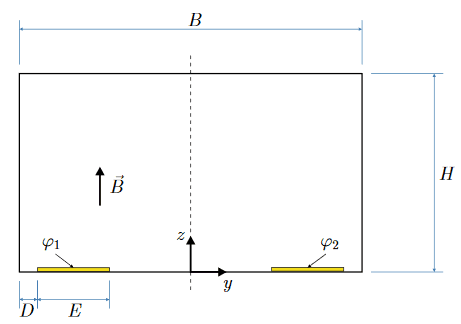
https://www.physicsforums.com/attachments/277981
 
Last edited:
Physics news on Phys.org
Is this a homework problem?
 
jasonRF said:
Is this a homework problem?
Yes. Is it in the wrong forum part?
 
Yes. There is a separate homework section. I have asked the moderators to move this thread over there.
 

Thread 'Initial conditions for orbits around a wormhole'

Hi, I had an exam and I completely messed up a problem. Especially one part which was necessary for the rest of the problem. Basically, I have a wormhole metric: $$(ds)^2 = -(dt)^2 + (dr)^2 + (r^2 + b^2)( (d\theta)^2 + sin^2 \theta (d\phi)^2 )$$ Where ##b=1## with an orbit only in the equatorial plane. We also know from the question that the orbit must satisfy this relationship: $$\varepsilon = \frac{1}{2} (\frac{dr}{d\tau})^2 + V_{eff}(r)$$ Ultimately, I was tasked to find the initial...
View full post »

Thread 'Help to convert units of a simple formula'

The value of H equals ## 10^{3}## in natural units, According to : https://en.wikipedia.org/wiki/Natural_units, ## t \sim 10^{-21} sec = 10^{21} Hz ##, and since ## \text{GeV} \sim 10^{24} \text{Hz } ##, ## GeV \sim 10^{24} \times 10^{-21} = 10^3 ## in natural units. So is this conversion correct? Also in the above formula, can I convert H to that natural units , since it’s a constant, while keeping k in Hz ?
View full post »

Similar threads

I Maxwell's equations PDE interdependence and solutions
Replies
5
Views
2K
I Why Lagrange’s method of solving Pp + Qq=R works?
Replies
3
Views
665
A Resistance Force on Gas in Magnetohydrodynamic Generator
Replies
2
Views
1K
Understanding Green's second identity and the reciprocity theorem
Replies
3
Views
5K
Understanding solution to equations of motion of n coupled oscillators
Replies
4
Views
2K
Derive the Maxwell "with source" equation
Replies
1
Views
1K
Relativistic electrodynamics: transformation of electric dipole moment
Replies
10
Views
1K
A How to solve simple 2D space-time PDE numerically
Replies
5
Views
3K
Deriving the wave equation using small perturbations
Replies
1
Views
1K
I Boundary Conditions for System of PDEs
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top