Magnitude and Component Question

[jegues]

Homework Statement

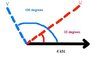
Determine the magnitude of the u and v-components of the 4kN force shown in the figure.

Homework Equations

The Attempt at a Solution

I'm confused, am I suppose to assign u and v a magnitude and direction in order to obtain a resultant force of 4kN horizontally?

The answers in the book are given as follows:

u = 4.11 kN
v = 2.44 kN

If I'm suppose to answer the question the way I think I do then,
<br /> Fy=Usin(35) + Vsin(105) = 0

Also,

<br /> Fx=Ucos(35) + Vcos(105) = 4

2 equations, 2 unknowns I can solve it but I don't think I'm doing this the right way, any ideas?

 

[vela]

I'm confused, am I suppose to assign u and v a magnitude and direction in order to obtain a resultant force of 4kN horizontally?

No, they're asking you to find the projection of F onto U and onto V. The projections won't add to equal F.

 

[jegues]

No, they're asking you to find the projection of F onto U and onto V. The projections won't add to equal F.

How do I go about finding the projection of F onto U and onto V? Also, I don't really know what you mean by projections so that might be what's stopping me from solving this problem.

 

[vela]

Sorry, I was wrong. I was thinking of a different problem. The two components will sum to F.

Did you finish solving for U and V the way you started? It looks okay to me.

 

[jegues]

So is my original "attempt" at the solution in my OP correct?

Also, it doesn't give the sense of the forces, only the line of action. It seems to me that this could have numerous possible solutions.

 

[vela]

I think your approach will work. The answer will be unique because the vectors along the U and V direction are linearly independent.

 

[jegues]

For V I get,

V = 10.12 and U,

U = 17.05

What do you think?

Also, are the answers in the book wrong?

 

[vela]

Those answers seem way off. I got different answers, but they don't match what your book got.

 

[jegues]

What'd you do?

I'm still not even sure if we're taking the right route to solving this question, or if we're even solving for the desired quantity.

I'm curious as to your approach.

 

[vela]

I solved your equations. :) I think you just made an algebra mistake when solving for U and V.

 

[jegues]

Hmmm the second time solving I got V = 20.78 and U = 35.

This any better?

 

[jegues]

My method for solving the problem doesn't seem to make any sense since both the Fy components would be positive and I need them to cancel out.

 

[vela]

No. Worse actually. You can check your answer by plugging it back into your equations and seeing if the sums work out correctly.

How are you solving the equations? I find Cramer's rule to be a good way to solve them.

 

[jegues]

I managed to solve it.

The answers the book indicated are correct, thanks for the help!

 

[vela]

Great! It turns out I was in radians mode, which is why I wasn't getting the correct answers.