Magnitude versus Frequency Response Drawing from Pole-Zero Plot

[Master1022]

Homework Statement

Sketch the frequency magnitude characteristics of the two analogue filters whose pole-zero configurations are shown in the figure. On the basis of these curves, what can you infer about the form of their impulse responses

Relevant Equations

Transfer functions

Hi,

EDIT: apologies for any ambiguity, but this is for DISCRETE systems, not analogue like the problem states.

I was attempting a problem which is shown below
.

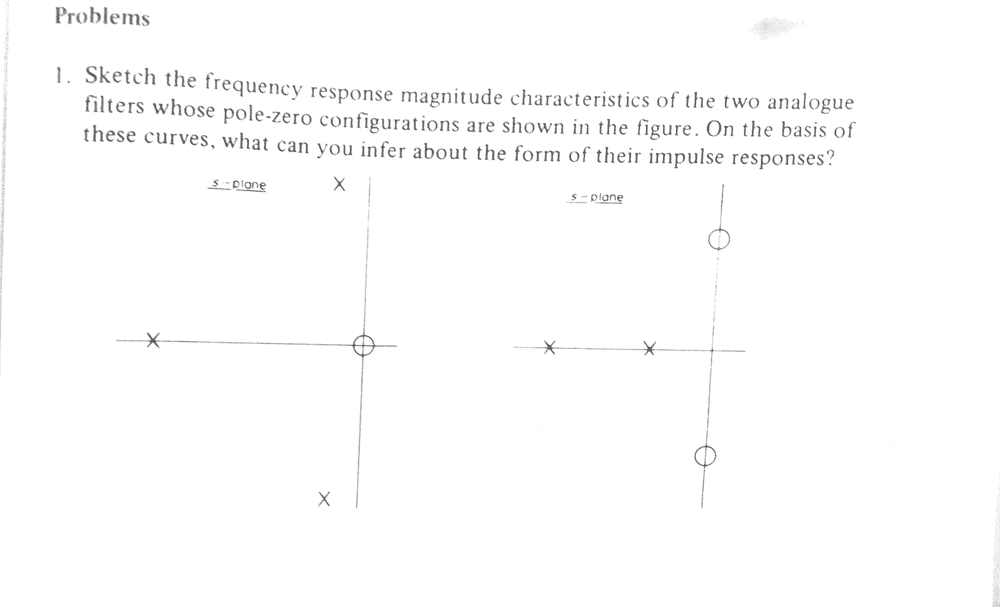
I am not really sure how to attempt this problem, but here is my attempt. Are there general methods for tackling these types of questions?

Attempt:
I have assumed that the outer most poles/zeros are on the unit circle such that the system is stable.

A zero on the unit circle will create a gain of zero at that frequency, whereas a pole will create resonance at its frequency. I think this because we can write the transfer function as:
$$ G(w) = \frac{\prod_{i = 1}^{n} |z-z_i|}{\prod_{j=1}^{m} |z-p_j|} $$

Part (a)
Thus, for the first (left) diagram, I think there should be resonance at the frequencies of the three poles. The effect of the zero is the same for all frequencies.

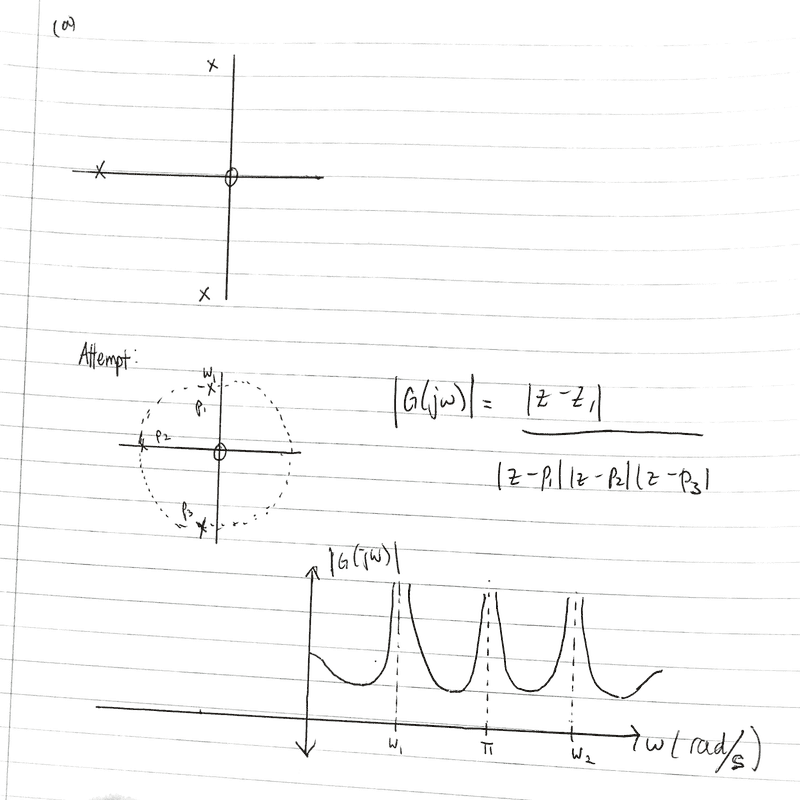
Part (b)
For the second (right hand) diagram, I think there should be resonance at the frequency of the outermost pole (the inner one is within the unit circle) and points of zero gain at the frequencies of the two zeros.

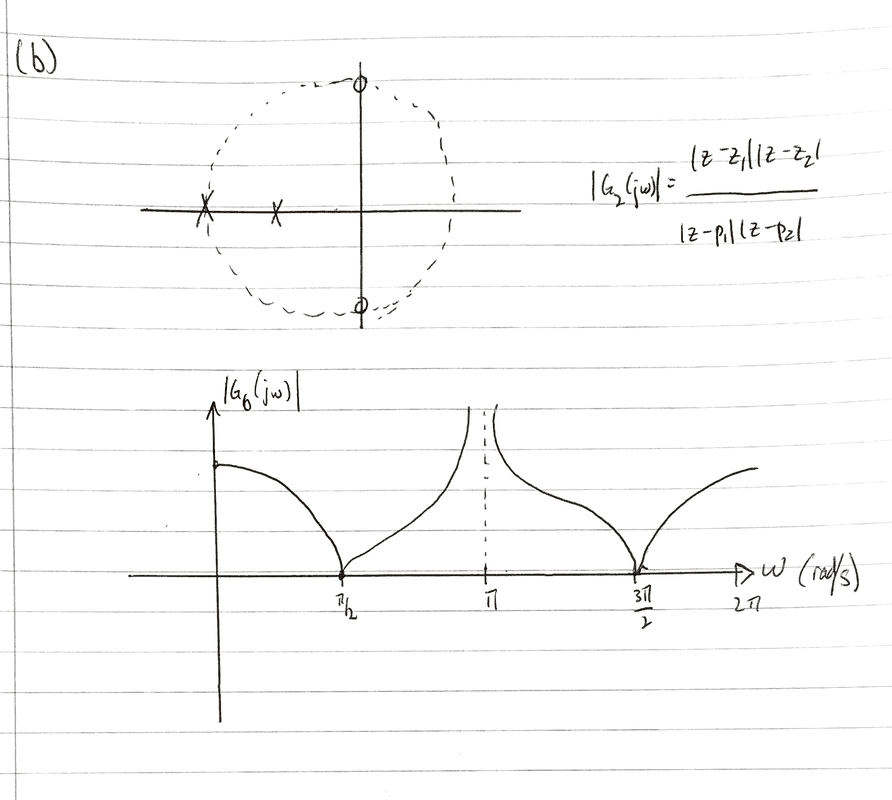
Are these attempts correct? If so, how I do make inferences about the impulse response from these?

I know that the impulse response is the transfer function, but am not sure how to qualitatively use these plots to describe it.

Thanks in advance for any help.

 

[DaveE]

No, not really correct. I think you need to go back and study your course materials a bit more to get this. It's hard to know how to provide guidance without knowing what the material that you've covered in your course is so far. But, I will start with some ideas:

Since you are being asked for the frequency response, then the terms in your magnitude equation like |(z-z_i)| can be written as |(jω-z_i)|. For frequency response, which is steady state, you will substitute z=jω. This can be visualized as the positive imaginary axis in the complex plane that you drew. At ω=0 you are at the origin. As ω increases (increasing frequency on your plot) you move up on the imaginary axis.

Now let's look at the term |(z-z_i)|. This can be visualized as the distance between z and z_i. So, for each frequency in your plot, you can measure the magnitude of jω-z_i for each pole or zero. You then multiply or divide these according to your magnitude formula.

You will do the same for the phase response, except you aren't multiplying the distance to the poles (or zeros), you are adding up the phase angles. So, for example, the angle from p2 to jω starts at 0 at ω=0 and increases as ω increases, approaching π/2 as ω→∞.

You do not necessarily get a resonance for each pole or zero. Resonance is a description of a rapid change in magnitude (and phase) as ω changes. This doesn't happen if the poles (or zeros) are always far from jω in the plane.

In the real world, roots with a non-zero imaginary part always come in complex conjugate pairs. Which are usually expressed as a quadratic term with real coefficients, like [1 + jω/(Qω_o) + (jω/ω_o)²]; but this may not be the style that applies to your course methods.

 

[Master1022]

Thanks for your reply!

No, not really correct. I think you need to go back and study your course materials a bit more to get this. It's hard to know how to provide guidance without knowing what the material that you've covered in your course is so far. But, I will start with some ideas:

Unfortunately we have had little to no teaching for this topic, so have just been trying to read on the internet. My knowledge is more or less restricted to the information (albeit incorrect) in the post.

Since you are being asked for the frequency response, then the terms in your magnitude equation like |(z-z_i)| can be written as |(jω-z_i)|. For frequency response, which is steady state, you will substitute z=jω. This can be visualized as the positive imaginary axis in the complex plane that you drew. At ω=0 you are at the origin. As ω increases (increasing frequency on your plot) you move up on the imaginary axis.

Apologies, but in the z-plane, doesn't $\omega = 0$ correspond to the point $1 + 0 j$ on the unit circle as $z = e^{sT} = e^{(\sigma + j\omega)T}$ and we are only concerned with $s = j \omega$ as you have written so $z = e^{j \omega T}$.

Now let's look at the term |(z-z_i)|. This can be visualized as the distance between z and z_i.

Agreed

So, for each frequency in your plot, you can measure the magnitude of jω-z_i for each pole or zero. You then multiply or divide these according to your magnitude formula.

I think my ambiguity in the post was not clear. Should this instead be $| e^{j \omega T} - z_i |$?

Does the fact that it is the z-plane change anything about the correctness (or lack thereof) about my method?

Thanks.

 

[DaveE]

in the z-plane, doesn't ω=0 correspond to the point 1+0j on the unit circle as z=esT=e(σ+jω)T and we are only concerned with s=jω as you have written so z=ejωT.

Yes, absolutely correct in discrete time z-plane. I missed that part of the problem, I thought it was continuous time, the s-plane in common usage.

 

[Master1022]

Yes, absolutely correct in discrete time z-plane. I missed that part of the problem, I thought it was continuous time, the s-plane in common usage.

Okay thank you very much. Do you know where I might be able to read about using the magnitude frequency plot to infer the behaviour of the impulse response?

 

[Master1022]

Yes, absolutely correct in discrete time z-plane. I missed that part of the problem, I thought it was continuous time, the s-plane in common usage.

Apologies, yes the problem statement had a typo and should have said discrete not analogue (quite the typo!)

 

[DaveE]

I'm not that "up to speed" with discrete filter design. It's been a few decades since I actually did any of that. I do think the concepts are similar though.

This guy has some nice videos though:

 

[DaveE]

Interesting that the problem statement doesn't have any scale associated with the pole locations. It's not such a big deal in the s-plane since it's the axes that matter. But, in the z-plane inside or outside the unit circle is a really important difference. Are you sure those poles are z-plane poles? The text says "analogue filter" and is labeled "s-plane". Sometimes the system is analog and the poles are described in continuous time, but the filter/controller is discrete time and you have to make the transformation at some point. I'm unclear on when/if discrete time matters here.

 

[Master1022]

Interesting that the problem statement doesn't have any scale associated with the pole locations. It's not such a big deal in the s-plane since it's the axes that matter. But, in the z-plane inside or outside the unit circle is a really important difference. Are you sure those poles are z-plane poles? The text says "analogue filter" and is labeled "s-plane". Sometimes the system is analog and the poles are described in continuous time, but the filter/controller is discrete time and you have to make the transformation at some point. I'm unclear on when/if discrete time matters here.

Hmm, that is true. We were told that it was a typo, but I will definitely check. I presume the problem was taken from somewhere and quickly repurposed to discrete time (perhaps without fully considering the nuances of the problem originally being set as an analogue)