Guillem_dlc
- 188
- 17
- Homework Statement
- The manometer in the figure contains two liquids A and B arranged as shown. Between the two liquids there is an area containing air. If the relative pressure of liquid A is ##p_A^r=-0,11\, \textrm{at}## and its relative density is ##\rho_A^r=1,6##, calculate the relative density ##\rho_B^r## of liquid B.
Solution: ##\rho_B=1##.
- Relevant Equations
- Equations of loops
Figure:
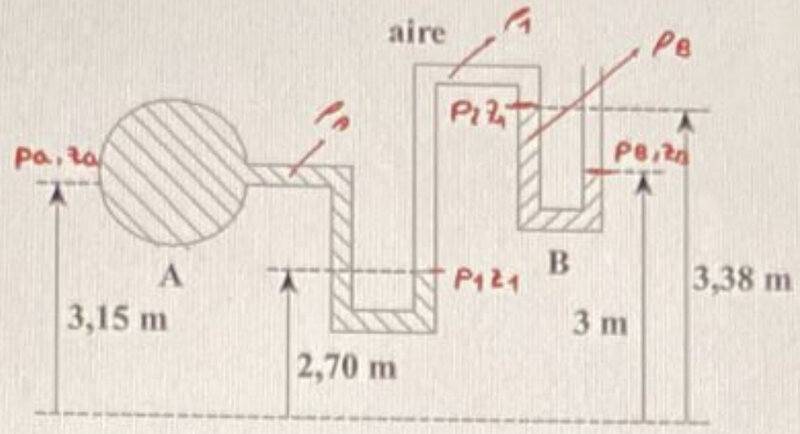
$$p_A^r=-0,11\, \textrm{at}\rightarrow p_A=90534\, \textrm{Pa}$$
$$\rho_A^r=1,6\rightarrow \rho_A=\rho_{AR}\cdot \rho_{H2O}=1600\, \textrm{kg}/\textrm{m}^3$$
$$\rho_1=1,225\, \textrm{kg}/\textrm{m}^3$$
$$\left.
\begin{array}{l}
\textrm{LOOP I}\rightarrow p_A-p_1=-\rho_A (Z_A-Z_1) \\
\textrm{LOOP II}\rightarrow p_1-p_2=-\rho_1(Z_1-Z_2) \\
\textrm{LOOP III}\rightarrow p_2-p_B=-\rho_B(Z_2-Z_B)
\end{array}\right\} \rightarrow$$
$$\rightarrow p_A-p_B=-\rho_A(Z_A-Z_1)-\rho_1(Z_1-Z_2)-\rho_B(Z_2-Z_B)\rightarrow$$
$$\rightarrow 90534-p_B=-720+0,833-\rho_B 0,38=-719,167-0,38\rho_B$$
In this exercise I am stuck because I don't know how to find the two missing unknowns.
$$p_A^r=-0,11\, \textrm{at}\rightarrow p_A=90534\, \textrm{Pa}$$
$$\rho_A^r=1,6\rightarrow \rho_A=\rho_{AR}\cdot \rho_{H2O}=1600\, \textrm{kg}/\textrm{m}^3$$
$$\rho_1=1,225\, \textrm{kg}/\textrm{m}^3$$
$$\left.
\begin{array}{l}
\textrm{LOOP I}\rightarrow p_A-p_1=-\rho_A (Z_A-Z_1) \\
\textrm{LOOP II}\rightarrow p_1-p_2=-\rho_1(Z_1-Z_2) \\
\textrm{LOOP III}\rightarrow p_2-p_B=-\rho_B(Z_2-Z_B)
\end{array}\right\} \rightarrow$$
$$\rightarrow p_A-p_B=-\rho_A(Z_A-Z_1)-\rho_1(Z_1-Z_2)-\rho_B(Z_2-Z_B)\rightarrow$$
$$\rightarrow 90534-p_B=-720+0,833-\rho_B 0,38=-719,167-0,38\rho_B$$
In this exercise I am stuck because I don't know how to find the two missing unknowns.