akhter900
- 5
- 0
...o..M
.... /|\
.Theta 2 /..|.\.Theta 1
.../...v..\
...F2 /...F...\.F1
.../.....\
.../... \
-----------|---------ground
...|...p...|
...v..f2.....v..f1
Hi every one,
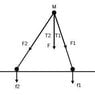
On the above diagram, M=10g is mounted on two fixed rods from the ground. So, the force acting on the point 'o' is F=10*9.8 = 98N. This force is going to distribute through the support as F1 and F2 and force on the ground for that two support will be f1 and f2. Here f1 is closer to p than f2. So, f1 should be grater than f2, ie. f1 > f2, is not it? Theta 1 = 30 degree and theta 2 = 45 degree.
To find out F1 and F2 I did something like,
F1 = F/Cos(30) = 113.16N
F2 = F/Cos(45) = 138.59N
Is it correct for force vector? I need to proof that F1 > F2.
I could not find out the distributed force F1 and F2 again f1 and f2 also. Is there anybody to give me some suggestions on this. I will be so grateful to you.
.... /|\
.Theta 2 /..|.\.Theta 1
.../...v..\
...F2 /...F...\.F1
.../.....\
.../... \
-----------|---------ground
...|...p...|
...v..f2.....v..f1
Hi every one,
On the above diagram, M=10g is mounted on two fixed rods from the ground. So, the force acting on the point 'o' is F=10*9.8 = 98N. This force is going to distribute through the support as F1 and F2 and force on the ground for that two support will be f1 and f2. Here f1 is closer to p than f2. So, f1 should be grater than f2, ie. f1 > f2, is not it? Theta 1 = 30 degree and theta 2 = 45 degree.
To find out F1 and F2 I did something like,
F1 = F/Cos(30) = 113.16N
F2 = F/Cos(45) = 138.59N
Is it correct for force vector? I need to proof that F1 > F2.
I could not find out the distributed force F1 and F2 again f1 and f2 also. Is there anybody to give me some suggestions on this. I will be so grateful to you.
Attachments
Last edited: