Santilopez10
- 81
- 8
- Homework Statement
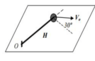
- Figure shows a body of mass ##m## laying on a frictionless table and subdued to interaction with a elastic band of natural lenght H and constant k, which is fixed to the origin ##O##. Suppose we give the object an initial velocity ##V_0## as shown in the image:
a) Obtain expressions for the transverse and radial components of the velocity vector as functions of the distance to O.
b) Suppose the radial component of the velocity is 0 at t=0. Find an expression for the maximum displacement of the elastic band.
- Relevant Equations
- .
a)
Our force can be represented as: $$\vec F= -k(r-H) \hat r$$ then the equations of motion are: $$\hat r: \ddot r -r {\dot{\theta}}^2=-\frac{k}{m_1}(r-H)$$ $$\hat{\theta}: r \ddot{\theta} + 2 \dot r \dot{\theta}=0$$
Plus we know that angular momentum is constant then $$|\vec L|=m r^2 \dot{\theta}$$
From the image we know that ##\vec{V_0}=\frac{V_0}{2} \hat r - \frac{\sqrt{3}}{2} V_0 \hat{\theta}## then at that instant ##\dot r=\vec {V_0}_{\hat r}=\frac{V_0}{2}## and ##\dot{\theta}=-\frac{\sqrt{3}}{2H} V_0## and we find the angular momentum of the system $$|\vec L|= \frac{\sqrt{3}}{2} m H V_0 = m r^2 \dot{\theta}$$
I have 3 equations for 4 unknowns, so I must be missing something. Plus, to be honest, I do not feel confortable with what I have done, I am not quite sure it is correct. Any help would be appreciated.
Our force can be represented as: $$\vec F= -k(r-H) \hat r$$ then the equations of motion are: $$\hat r: \ddot r -r {\dot{\theta}}^2=-\frac{k}{m_1}(r-H)$$ $$\hat{\theta}: r \ddot{\theta} + 2 \dot r \dot{\theta}=0$$
Plus we know that angular momentum is constant then $$|\vec L|=m r^2 \dot{\theta}$$
From the image we know that ##\vec{V_0}=\frac{V_0}{2} \hat r - \frac{\sqrt{3}}{2} V_0 \hat{\theta}## then at that instant ##\dot r=\vec {V_0}_{\hat r}=\frac{V_0}{2}## and ##\dot{\theta}=-\frac{\sqrt{3}}{2H} V_0## and we find the angular momentum of the system $$|\vec L|= \frac{\sqrt{3}}{2} m H V_0 = m r^2 \dot{\theta}$$
I have 3 equations for 4 unknowns, so I must be missing something. Plus, to be honest, I do not feel confortable with what I have done, I am not quite sure it is correct. Any help would be appreciated.