guss
- 246
- 0
Energy (a joule) is defined as
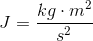
So, the definition of energy involves kilograms. However, because of E = mc^2, mass is another way of writing energy, or the same thing as energy.
It seems to me like this should bring up some sort of contradiction. If mass and energy go back and forth defining each other, isn't nothing really defined in the end? Like some sort of endless loop?
Just spilling out thoughts here. Anyone have any ideas?
So, the definition of energy involves kilograms. However, because of E = mc^2, mass is another way of writing energy, or the same thing as energy.
It seems to me like this should bring up some sort of contradiction. If mass and energy go back and forth defining each other, isn't nothing really defined in the end? Like some sort of endless loop?
Just spilling out thoughts here. Anyone have any ideas?
Last edited: