Mass hanging by spring tracing a eight shaped curve

[Saitama]

Homework Statement

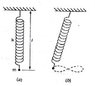
A mass $m$ on the end of a light spring of force constant $k$ stretches the spring to a length $l$ when at rest. The mass is now set into motion so it executes up and down vibrations while swinging back and forth as a pendulum. The mass moves in a figure-eight pattern in a vertical plane, as shown in the figure. Find the force constant in terms of $m$,$l$ and $g$.

(Ans: k=4mg/l )

Homework Equations

The Attempt at a Solution

I noticed that the curve traced by the hanging mass is of the form $r^2=a\cos(2\theta)$ with the mass $m$ being at the origin at $t=0$. But I don't think this is going to help. This is a question from one of my practice sheets and I doubt I need to deal with polar curves which aren't generally taught in high school.

How do I approach this problem?

Any help is appreciated. Thanks!

 

[jedishrfu]

Since it traces out a figure eight that would suggest that one oscillation is twice what the other oscillation is so maybe you can factor that into your solution.

 

[andrevdh]

Lets me think of Lissajous figures. For a figure 8 the frequencies of oscillations are 1:2. In this case the up-down oscillations are twice those of the pendulum motion. Not sure this helps or is relevant though.

 

[Saitama]

Since it traces out a figure eight that would suggest that one oscillation is twice what the other oscillation is so maybe you can factor that into your solution.

Ah yes, thanks a lot jedishrfu! :)

$$2\times 2\pi\sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{l}{g}}$$
$$\Rightarrow k=\frac{4mg}{l}$$

 

[andrevdh]

I think the springs' frequency of oscillations is twice that of the pendulum in this case.