Mass wraps around rod in circular motion

[unscientific]

Homework Statement

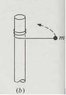
A string attached to the center of a rod with radius R has a mass attached at the other end, moving with speed v₀. Because of acceleration due to gravity the mass moves down while undergoing circular motion, causing the string to wrap around the rod. Find an expression for the time taken for the string to completely wrap around the rod.

Homework Equations

v = rw

The Attempt at a Solution

-constant tangential velocity since acceleration due to gravity acts only downwards
-w = v/r, so as the string wraps around the rod, the angular velocity increases

w_(t) = v₀/r_(t)

-w_(t) is the same along all lengths of the string

-tried to figure out dr/dt, but to no avail

 

[supratim1]

use energy conservation, where x is the distance moved downwards by the mass, so

mgx = 1/2 mv^2 + 1/2 Iw^2

and use, w = v/r

 

[unscientific]

use energy conservation, where x is the distance moved downwards by the mass, so

mgx = 1/2 mv^2 + 1/2 Iw^2

and use, w = v/r

hmm, i don't really understand how the term '1/2 Iw^2' comes about - the tangential velocity stays the same, all its doing is accelerating downwards

Loss in GPE = Gain in KE
mgx = 1/2 mv_y^2 (in the y-direction)

I'm interested in finding out the time taken for a given string of length l to finish wrapping a rod of radius R entirely.

-at every point in time the mass is undergoing circular motion
-fixed tangential velocity, but increasing angular velocity
-in order to find the time taken to wrap around the rod, i must find an expression for dl/dt, where l is the length of the string. I imagine it to be some function of (r,v₀ and t)

 

[unscientific]

it's okay, i solved it! :)