Mastering Kirchhoff's Law: Solving for 5 Currents in a Complex Circuit

[BlasterV]

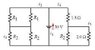
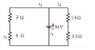
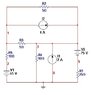
The point is to find currents i1,2,3,4, and 5 in the picture.

R1 = 14 Ohms
R2 = 6 Ohms

This is my work so far.
5 Currents, 5 Loops, 5 Equations, that is the rule (or so I think)

The way I am looking at it, there are 6 Loops, so if someone could reduce it to 5 that'd be of some help right there.

My second problem is that it is clear i1 branches off to i2 and i4, thus:
i1 = i2 + i4
but I don't know how to account for i3 and i5 in this equation, if someone could help me with that it'd be of great help too.

While I'm not exactly sure how the algebra works either I think I can figure it out if the 5 loops are identified and the quantities of the i's in comparison to each other are explained.

Anyhow, thanks for any help you can give, I know this is kind of a dreaded topic =P

 

[mezarashi]

Well I would suppose that it becomes "really hard" when you are using a "really hard" approach. Circuit analysis (especially with only resistors) will probably be one of the easiest subject you will ever take (once you understand it and reflect back a few years later). For this question, there are 5 loops. If you are solving it using Mesh Analysis, then you are in for a run. While this approach will theoretically work, a lot of calculations are needed. Instead, if you count carefully the nodes, there are only 3 nodes. Namely, the ground + 30V supernode, the node between R1 and R2 on the left, and the node between R2 and 1.5 on the right. Use KCL on these nodes.

incoming current = outgoing current

The current across any resistor element is equal to the potential difference divided by the resistance value. I = (V2-V1)/R

 

[FluxCapacitator]

Kirchoff problems are hard algebraicly, but finding the equations shouldn't be too difficult. You seem to have mastered the current branching equations, (i1=i2+i4), but you also need to know this one:

\epsilon - \sigma i_{n}r_{n}=0 over a closed loop.

To use the above equation, just make some closed loop that has the battery on your diagram. Then take the emf, 30 V, and subtract each 'potential drop' as you go around the loop. You can do this with however many loops you want until you have enough equations to do one gigantic system of equations and solve for your unknowns. The solving isn't too fun, but this is one of the few areas in physics (thus far at least) where you can just pick a random loop of your choice to do the problem. If you're still confused, post another message, and I'll try to clarify.

Also, I'll try to do this problem when I'm not busy later today.

 

[BlasterV]

What is KCL?

Edit: Wait I think you mean Kirchhoff's law lol my bad.

 

[mezarashi]

Kirchoff's Current Law.

incoming current = outgoing current

or the law of conservation of charge. With KVL (Kirchoff's Voltage Law): voltage around any closed loop is always zero, an interpretation of Gauss's Law. Also a type of conservation of energy so that perpetual machines cannot be allowed.

 

[BlasterV]

Ok using just the three nodes I cameup with 3 equations:

i1 = i2 + i4

30V - 14ohm*i2 - 6ohm*i2 = 0
30 - 1.5*i4 - 6*i4 = 0

I solved them to come up with

i4 = 4 A
i1 = 5.5 A
i2 = 1.5 A

But all are wrong, I am sure I am missing something big especially since i3 and i5 are unaccounted for, am I getting the loops/relation between Rs and Is wrong?

 

[mezarashi]

You continue to use KVL instead of KCL. The units of your terms are in volts. When you use KCL (nodal analysis), the units will be in amps. If you'd like to solve this problem using mesh analysis although it is more difficult to do so, do say so. In nodal analysis, we have then at node 1, which we will denote V1 (an unknown voltage we would like to find).

(30-V1)/R1 + (30-V1)/R1 = (V1-0)/R2 + (V1-0)/R2
it can be simplified

Our second equation at node 2, with voltage V2 (also unknown):

(30-V2)/1.5 = (V2-0)/R2 + (V2-0)/2.0

You have 2 unknowns, V1, and V2, and 2 equations. Solved.

Now you refer back to the original question of finding i2,3,4,5. This becomes a very trivial deal with all voltages at all nodes known. As the current is defined as: I = (delta V)/R.

So for example i3 = (V1-0)/R2 and i5 = (V2-0)/2.0

 

[leright]

Jesus dude, you can reduce that network down significantly. Look for all of the parallel resistor combinations. Once you combine some of the parallel resistors you have even more resistors in series. Once you simplify the circuit by network reduction it is a piece of cake and can be solved easily using kirchhoffs laws. the key is to make any parallel/series reductions before solving the circuit.

 

[Ahmed Basha]

What about reducing the network ?

I had an idea to reduce the network. It came up to a very simple network and very logic solution.
Please, see the attached picture.

The solution which came up was:
i1= 13 Amp
i2= 3 Amp
i3= 1.5 Amp
i4= 10 Amp
i5= 7.5 Amp

 

[leright]

I had an idea to reduce the network. It came up to a very simple network and very logic solution.
Please, see the attached picture.

The solution which came up was:
i1= 13 Amp
i2= 3 Amp
i3= 1.5 Amp
i4= 10 Amp
i5= 7.5 Amp

This thread was created over two years ago...

 

[Ahmed Basha]

I read it just one week ago. HeHeHeHeHe :)

 

[smash]

Where's I5?

 

[smash]

Help

How Would I Work Out The Solution Given That There Are Current Sources In This Circuit.. And TO CALC The Power Dissapated In The R3 Resistor.

Regards

 

[The Electrician]

This circuit just cries out to make some Thevenin/Norton transformations. You could transform the two current sources (plus their associated parallel resistors) into Thevenin equivalents and then do a loop analysis, or you could transform the two voltage sources (plus their series resistors) into Norton current source equivalents and do a nodal analysis.
Try one of those and post your results. If you're still having trouble, then I'll follow up.