MATLAB - floating point numbers

AI Thread Summary
The discussion revolves around solving two equations using MATLAB's symbolic capabilities and comparing results obtained with integer versus floating-point definitions. Users noted that their outputs remained identical regardless of whether they used integers or floating-point numbers, which led to confusion about expected variations in results. It was suggested that the digits() function could alter the precision of symbolic data, but some participants were unfamiliar with its application. Additionally, there was mention of using the syms function for variable definitions, which could potentially improve the clarity of the symbolic computations. Overall, the conversation highlights challenges in understanding MATLAB's symbolic math toolbox and the nuances of floating-point arithmetic.
GreenPrint
Messages
1,186
Reaction score
0

Homework Statement



Consider the following two equations:

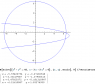
x^2 + y^2 = 42
x + 3y + 2y^2 = 6

Define a symbolic equation for each, and solve it by using MATLAB's symbolic capability. Could you solve these equations by using matrices? Try this problem twice, once using only integers in your equation definitions and once using floating-point numbers (those with decimal points). how do your results vary? Check the workspace window to determine weather the results are still symbolic.

Homework Equations





The Attempt at a Solution



I think that I may be doing something wrong because when I wrote out my code and ran it I got the same exact results when I tried using integers and when I included decimal points. I was hoping someone could explain to me what I'm doing wrong because I guess I'm suppose to get different results.

Code: 
>> disp('No you could not solve this problem usign matrices.')
one=sym('x^2+y^2-42');
two=sym('x+3*y+2*y^2-6');
[x,y]=solve(one,two)
one=sym('x^2.0+y^2.0-42.0');
two=sym('x+3.0*y+2.0*y^2.0-6.0');
[x,y]=solve(one,two)
No you could not solve this problem usign matrices.
 
x =
 
 -6.2161908711674029137999766546085
  6.4782037201238076694174751205659
  6.3321946913754454971273459117746
  -5.594207540331850252744844377732
 
 
y =
 
   1.8327495882457713513416277757555
 -0.18131894709064188368251606877471
  -1.3796051574695662000556283784362
  -3.2718254836855632676034833285446
 
 
x =
 
 -6.2161908711674029137999766546085
  6.4782037201238076694174751205659
  6.3321946913754454971273459117746
  -5.594207540331850252744844377732
 
 
y =
 
   1.8327495882457713513416277757555
 -0.18131894709064188368251606877471
  -1.3796051574695662000556283784362
  -3.2718254836855632676034833285446

Thanks in advance!
 
Physics news on Phys.org
you can change the accuracy of symbolic data with digits() otherwise this is its default output.
 
Interesting. Are textbook hasn't covered the digits function yet. I'll go look up how to use it.
 
I'm confused as to how to use the digits function and incorporating it into this problem.
 
I'm not really familiar with the Symbolic Math Toolbox, but a quick search at the Mathworks' MATLAB documentation page brings up the following:
http://www.mathworks.com/help/toolbox/symbolic/f1-5556.html

If you don't already know, you can also access abridged documentation from the MATLAB command prompt by typing in help <function>. For instance:
>> help digits
 
Last edited by a moderator:
It's my understand that digits(x) just changes how many digits are displayed in results to x. At least that's what function seems to do and what the help document says. I thought i was suppose to get different results when I did 5*x and 5.0*x or something. I'm pretty sure I don't need the digits function as this is the first time I have come across it. Hmm...
 
I was expecting something along the lines of

Code: 
>> solve('5.0*x^2.0+6.0*x-7.0')
solve('5*x^2+6*x-7')
 
ans =
 
 0.72665
 -1.9266
 
 
ans =
 
   (2*11^(1/2))/5 - 3/5
 - (2*11^(1/2))/5 - 3/5
were the results actually varied
 
Odd, the lab computer here seems to produce the correct result:

Code: 
x =
 
[ 33/4-1/4*3^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)-1/4*6^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)-((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)*(2033+18*i*71413^(1/2))^(2/3)-301*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+9*3^(1/2)*(2033+18*i*71413^(1/2))^(1/3))/(2033+18*i*71413^(1/2))^(1/3)/((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2))^(1/2)-2*(-3/4+1/12*3^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+1/12*6^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)-((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)*(2033+18*i*71413^(1/2))^(2/3)-301*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+9*3^(1/2)*(2033+18*i*71413^(1/2))^(1/3))/(2033+18*i*71413^(1/2))^(1/3)/((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2))^(1/2))^2]
[ 33/4-1/4*3^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+1/4*6^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)-((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)*(2033+18*i*71413^(1/2))^(2/3)-301*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+9*3^(1/2)*(2033+18*i*71413^(1/2))^(1/3))/(2033+18*i*71413^(1/2))^(1/3)/((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2))^(1/2)-2*(-3/4+1/12*3^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)-1/12*6^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)-((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)*(2033+18*i*71413^(1/2))^(2/3)-301*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+9*3^(1/2)*(2033+18*i*71413^(1/2))^(1/3))/(2033+18*i*71413^(1/2))^(1/3)/((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2))^(1/2))^2]
[   33/4+1/4*3^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)-1/4*(-(-330*(2033+18*i*71413^(1/2))^(1/3)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+6*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)*(2033+18*i*71413^(1/2))^(2/3)+1806*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+54*3^(1/2)*(2033+18*i*71413^(1/2))^(1/3))/(2033+18*i*71413^(1/2))^(1/3)/((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2))^(1/2)-2*(-3/4-1/12*3^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+1/12*(-(-330*(2033+18*i*71413^(1/2))^(1/3)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+6*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)*(2033+18*i*71413^(1/2))^(2/3)+1806*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+54*3^(1/2)*(2033+18*i*71413^(1/2))^(1/3))/(2033+18*i*71413^(1/2))^(1/3)/((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2))^(1/2))^2]
[   33/4+1/4*3^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+1/4*(-(-330*(2033+18*i*71413^(1/2))^(1/3)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+6*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)*(2033+18*i*71413^(1/2))^(2/3)+1806*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+54*3^(1/2)*(2033+18*i*71413^(1/2))^(1/3))/(2033+18*i*71413^(1/2))^(1/3)/((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2))^(1/2)-2*(-3/4-1/12*3^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)-1/12*(-(-330*(2033+18*i*71413^(1/2))^(1/3)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+6*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)*(2033+18*i*71413^(1/2))^(2/3)+1806*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+54*3^(1/2)*(2033+18*i*71413^(1/2))^(1/3))/(2033+18*i*71413^(1/2))^(1/3)/((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2))^(1/2))^2]
 
 
y =
 
[ -3/4+1/12*3^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+1/12*6^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)-((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)*(2033+18*i*71413^(1/2))^(2/3)-301*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+9*3^(1/2)*(2033+18*i*71413^(1/2))^(1/3))/(2033+18*i*71413^(1/2))^(1/3)/((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2))^(1/2)]
[ -3/4+1/12*3^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)-1/12*6^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)-((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)*(2033+18*i*71413^(1/2))^(2/3)-301*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+9*3^(1/2)*(2033+18*i*71413^(1/2))^(1/3))/(2033+18*i*71413^(1/2))^(1/3)/((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2))^(1/2)]
[  -3/4-1/12*3^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+1/12*(-(-330*(2033+18*i*71413^(1/2))^(1/3)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+6*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)*(2033+18*i*71413^(1/2))^(2/3)+1806*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+54*3^(1/2)*(2033+18*i*71413^(1/2))^(1/3))/(2033+18*i*71413^(1/2))^(1/3)/((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2))^(1/2)]
[  -3/4-1/12*3^(1/2)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)-1/12*(-(-330*(2033+18*i*71413^(1/2))^(1/3)*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+6*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)*(2033+18*i*71413^(1/2))^(2/3)+1806*((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2)+54*3^(1/2)*(2033+18*i*71413^(1/2))^(1/3))/(2033+18*i*71413^(1/2))^(1/3)/((55*(2033+18*i*71413^(1/2))^(1/3)+2*(2033+18*i*71413^(1/2))^(2/3)+602)/(2033+18*i*71413^(1/2))^(1/3))^(1/2))^(1/2)]

EDIT: Also, have you tried using the x=syms('x') and y=syms('y') approach? I should add that we have an ancient copy of MATLAB here, R13 (v6.5)
 
I'm not sure what exactly you mean by incoperating x=syms('x') and y=syms('y') approach?

I thought syms was for creating symbolic representations of variables and you just did
syms x y
I'm not exactly sure what x=syms('x') and y=syms('y') even does

Code: 
>> x=syms('x')
? Error using ==> syms
Too many output arguments.

I don't think I follow.

also I'm using MATLAB 7.12.0(R2011a)
 
  • #10
Ah, syntax changed. If you read the link in my previous post, you'll see that the proper syntax is:

Code: 
syms x y
one=x^2+y^2-42
two=x+3*y+2*y^2-6
[x,y]=solve(one, two)
 
  • #11
Code: 
>> syms x y
one=x^2+y^2-42
two=x+3*y+2*y^2-6
[x,y]=solve(one, two)
 
one =
 
x^2 + y^2 - 42
 
 
two =
 
2*y^2 + 3*y + x - 6
 
 
x =
 
 -6.2162
  6.4782
  6.3322
 -5.5942
 
 
y =
 
   1.8327
 -0.18132
  -1.3796
  -3.2718
=(

It only went out to 5 digits from when I was experimenting with the digit function I did digit(5)
 
  • #12
In this matter, MATLABdude is a MATLABdud.

Have you tried the CS solution? Exit MATLAB and then start it up again?
 
  • #13
I don't know what you mean by CS, but I tried exiting and restarting MATLAB and the same results occurred.
 
  • #14
Does anyone have any other solutions that might work?
 
  • #15
hmm... I find it odd that it worked properly in a older version of MATLAB >_>
 
  • #16
could someone please confirm with a newer version of MATLAB that there getting the same results?
 
  • #17
still stuck
 
  • #18
Can someone with a newer version of MATLAB please run my code and let me know what results they get?
 
  • #19
GreenPrint said:
Does anyone have any other solutions that might work?

Using Mathematica, I see that the problem amounts to finding the intersections between a circle and a parabola. There are only 4 intersections, so I would expect 4 solutions.

See the attachment:
 

Attachments

  • Prob1.png
    Prob1.png
    6.7 KB · Views: 562
  • #20
ya i was expecting to get an exact result though as the other person and not a rounded answer though
 
  • #21
I'm still trying to get MATLAB to give me the exact results as the other person did but I can't seem to get MATLAB to do so...

I'm trying to get MATLAB to give me the exact results by trying to get around this in some other way... I have noticed one thing

x^2 + y^2 = 42
x + 3y + 2y^2 = 6

the second equation is linear
x + 3y + 2y^2 = 6
x=6-3y-2y^2
and i can substitute into the first equation
x^2 + y^2 = 42
x=6-3y-2y^2

(6-3y-2y^2)^2+y^2=42
but
Code: 
solve('(-3*y + -2*y^2 + 6 )^2 + y^2 = 42','y')
 
ans =
 
   1.8327495882457713513416277757555
 -0.18131894709064188368251606877471
  -1.3796051574695662000556283784362
  -3.2718254836855632676034833285446
no cigar... any suggestions would be greatly appreciated
 

Similar threads

Solving System of Equations Using Matrices
Replies
1
Views
4K
Solving a System of 2 ODES with Interval conditions
Replies
1
Views
2K
Using Newton's Method to Solve and Using Fsolve in Matlab
Replies
2
Views
2K
Problem with plotting a function in MATLAB
Replies
10
Views
2K
Linear Algebra: Matlab Question
Replies
1
Views
2K
MATLAB: with My Fixed Point Iteration Program
Replies
1
Views
20K
Finding the Equation of a Plane from 3 Coplanar Points
Replies
1
Views
1K
Does the angle of a beam fixed at two points affect the method?
Replies
3
Views
2K
Linear Equation System Solution and Matrix Multiplication in MATLAB
Replies
2
Views
1K
Using 'solve' command in MATLAB R2008a
Replies
5
Views
5K

Hot Threads

Recent Insights

Back
Top