csc
- 2
- 0
Homework Statement
Hi,
I am new to MATLAB and have an assignment where I have to construct a Hamiltonian matrix, apply boundary conditions, then find corresponding eigenvalues and eigenvectors for the electron in a box problem. I am stumped where to start. From our class we learned that you will get to the equation
-h_bar^2/2m[psi_(i+1)-2psi_(i)-psi_(i-1)] by using the definition of a derivative and can use the boundary conditions to manipulate this equation to give you the coefficients to use in the hamiltonian matrix, however, it does not seem like we need this because it will be applied when we set the limits for the Hamiltonian. Any advice on a good start would be greatly appreciated.
Attached is the pdf of the problem.
Homework Equations
HΨ=EΨ
The Attempt at a Solution
I was suggested by my professor to start here:
In your code, you have to create an empty matrix that you will use as a Hamiltonian (let’s call H), and then assign the elements. For example, in MATLAB, you can do something like below.
H(1,1) = -2*t_0;
H(1,2) = t_0;
H(1,3) = 0;
H(1,4) = 0;
I believe you know what t_0 is. Since we don’t want to do all this manually one by one, you can use “for” or “while” syntax to define H more easily. Once you fill up H correctly (remember, when you do this, you would have already applied the boundary condition. Review how different boundary conditions have resulted in different Hamiltonian), you simply perform eig function. To do this, you will need to create two empty matrixes that will contain the calculated eigen vectors and eigen values. In your previous email, you said you learned how to use [V, D] = eig (H). So, for example, V will contain the eigen vectors (eigen functions) and D will contain the eigen values after you execute the line in your code.
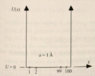
You know that you have to define many “constants” in your code. t_0 contains del_x which is the lattice spacing (I think I used del_x in my lecture instead of a, but here I mean del_x by a. N is the number of total lattice points (=100). So the situation is something like this. (see attached picture)