- #1
kostoglotov
- 234
- 6
MIT OCW 18.06 Intro to Linear Algebra 4th edt Gilbert Strang
Ch6.2 - the textbook emphasized that "matrices that have repeated eigenvalues are not diagonalizable".

imgur: http://i.imgur.com/Q4pbi33.jpg
and
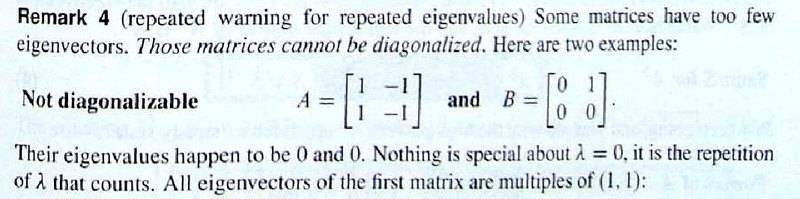
imgur: http://i.imgur.com/RSOmS2o.jpg
Upon rereading...I do see the possibility to interpret this to mean that fewer than n independent eigenvectors leads to an undiagonalizable matrix...that n-all different eigenvalues ensures n-independent eigenvectors...leaving open the possibility of n-independent eigenvectors with repeated eigenvalues...? Yes, no?
Because the second worked example shows a matrix with eigenvalues 1,5,5,5, and the use of diagonalization of that matrix, and Matlab is quite happy to produce a matrix of n-independent eigenvectors from this matrix.
The matrix in question is 5*eye(4) - ones(4);
What is the actual rule, because I don't feel clear on this.
Ch6.2 - the textbook emphasized that "matrices that have repeated eigenvalues are not diagonalizable".
imgur: http://i.imgur.com/Q4pbi33.jpg
and
imgur: http://i.imgur.com/RSOmS2o.jpg
Upon rereading...I do see the possibility to interpret this to mean that fewer than n independent eigenvectors leads to an undiagonalizable matrix...that n-all different eigenvalues ensures n-independent eigenvectors...leaving open the possibility of n-independent eigenvectors with repeated eigenvalues...? Yes, no?
Because the second worked example shows a matrix with eigenvalues 1,5,5,5, and the use of diagonalization of that matrix, and Matlab is quite happy to produce a matrix of n-independent eigenvectors from this matrix.
The matrix in question is 5*eye(4) - ones(4);
What is the actual rule, because I don't feel clear on this.