Max. n for TIR - air-medium interface

[psyphy]

Homework Statement

A light ray in air is obliquely incident on a parallel-sided slab of refractive index 'n'.
The light ray refracts and hits the left side of the slab and undergoes total internal refraction.
What is the maximum possible 'n' value?

NOTE - This is a theoretical problem that I created upon observation of a numerical problem that asks for range of incident angles. I do not know if maximum 'n' value can exist for any given circumstances. Also, I have neglected the fact that at critical angle incidence, T.I.R. doesn't occur. However, a small dθ after c should cause T.I.R, so I have left out that negligible amount. Please point out any clarification and/or errors in my assumptions.

Homework Equations

n * sin θ = constant
sin c = 1 / n

The Attempt at a Solution

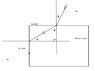
Now, assume the ray is incident at angle i on the top side.
Upon refraction, we can say → sin i = n * sin r.
Also, since maximum value of sin() is 1; sin i < 1 → n * sin r < 1
( we disregard i = 90°, as the ray is obliquely incident on, and not grazing, the slab)

Now, for air-slab interface, of critical angle c, we know that sin c = 1 / n.
Also, when we draw a diagram, the normals to the incident ray and refracted, T.I.R-ing ray form a right triangle, with c and r as the other two angles → c + r = 90° → c = 90° - r
Taking sin() on both sides, we get sin c = sin (90° - r) = cos r
OR, cos r = 1 / n → sin r = √(1 - ( 1 / n^2 ) ) → n * sin r = √( n^2 - 1)
OR, √( n^2 - 1) < 1 → n^2 < 2 → n < √2

Therefore, the maximum value for 'n', for ray at air-slab interface to undergo T.I.R, is √2.

 

[psyphy]

Bump?...

 

[truesearch]

Your diagram is wrong angle r should be less than angle i

 

[psyphy]

@truesearch -

My apologies! I rushed through while making the diagram on Paint.NET.

Regardless, what do you think of the proof?

 

[ehild]

The result is correct, but the proof is not mathematically rigorous.
So sinr≤1/n, cos(r)≤1/n...

ehild

 

[psyphy]

What exactly does that mean?

What are the implications of this proof and your counter-arguments?

I'm a bit confused...

 

[ehild]

For total reflection, 90-r, the angle of incidence at the side of the slab must be greater than or equal to the critical angle θ_c even with the greatest r, which is equal to θ_c

90°-r≥θ_c,→ r≤90°-θ_c even for the greatest r:

r ≤θ_c≤90°-θ_c→ θ_c≤45°

The sine function is monotonously increasing between 0°and 90° so

sinθ_c=1/n≤1/√2 →n≥√2:

the refractive index can not be smaller than √2. √2 is the smallest, the minimum refractive index that ensures total reflection. There is no maximum refractive index. It can be arbitrary greater than √2.

ehild