Maximizing Angular Velocity to Prevent Slipping in a Rotating Cylinder Ride

[lemaitre]

A fairground ride takes the form of a hollow, cylinder of radius R rotating about its axis. People lie down cylinder wall when it is stationary. The rotation is then started, and once the cylinder has reached its operating angular velocity \omega, its axis, and the people, are gradually rotated, as shown in the figure below.

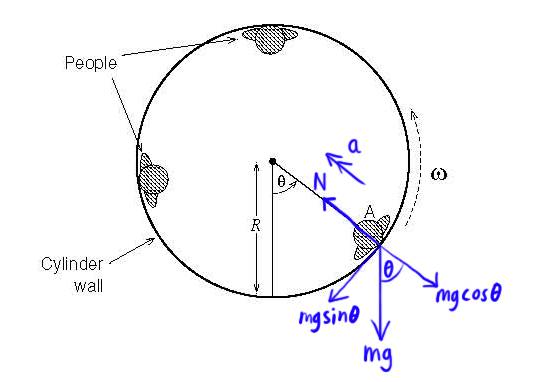
Figure above shows a view along the axis in a horizontal direction showing the heads and shoulders of three people, who face inwards. Thus the person at the top is facing vertically downwards at the moment shown.

A person called Alice who has mass m, is indicated by A in the figure at the moment when she subtends angle \theta relative to the downwards vertical direction, as seen from the cylinder’s axis. Assuming that Alice does not slide relative to the cylinder wall, and neglecting her size compared to the radius R.

1. Show that the component of force upon Alice from the cylinder wall normal to its surface is given by N = mg\cos\theta +m\omega^{2}R.

Answer

The acceleration is towards the center of the cylinder, hence

\sum{F}=ma \Rightarrow N - mg\cos\theta = ma \Rightarrow N = mg\cos\theta + m\omega^{2}R.
​

2. Show that the component of force upon Alice from the cylinder wall parallel to its surface is given by F = mg\sin\theta.

Answer

This follows from the diagram.

3. Derive an expression for the minimum \omega required to ensure that Alice remains in contact with the cylinder wall at all times.

4. Show that in order for Alice to avoid sliding along the cylinder wall, \omega^{2} \geq \frac{g\sin\theta}{\mu_{S}R} - \frac{g\cos\theta}{R}, where \mu_{S} is the coefficient of static friction between her and the wall.

Answer

f_{S} \leq\mu_{S}N \Rightarrow mg\sin\theta \leq \mu_{S}(mg\cos\theta +m\omega^{2}R). Rearranging, we get \omega^{2} \geq \frac{g\sin\theta}{\mu_{S}R} - \frac{g\cos\theta}{R}.

5. Use the result of question 4 to show that Alice will not slip for any \theta if \omega^{2} \geq \frac{g}{R}\sqrt{1 + \frac{1}{\mu_{S}^{2}}}.Question and Attempt

I would like to know if the working for the questions above that I have answered are correct. I'm not sure what concept underlies question 3. For question 5, I put \theta = \pi, the angle that subtends when she is at the top but that doesn't work.

I'm looking for hints to be able to answer questions 3 and 5. Thank you for your time.

 

[cepheid]

Welcome to Pf lemaitre!

For question 3: the normal force is, by definition, the contact force between two surfaces. So, if Alice is no longer in contact with the cylinder wall, it must be true that N = 0. That's the concept.

EDIT: this thread belongs in intro physics. Moved.

 

[lemaitre]

Welcome to Pf lemaitre!

For question 3: the normal force is, by definition, the contact force between two surfaces. So, if Alice is no longer in contact with the cylinder wall, it must be true that N = 0. That's the concept.

EDIT: this thread belongs in intro physics. Moved.

Thank you cepheid.

So for Alice to remain in contact with the cylinder wall, N \gt 0.

N = mg\cos\theta + m\omega^{2}R, so N \gt 0 \Rightarrow mg\cos\theta + m\omega^{2}R \gt 0 \Rightarrow \omega \gt \sqrt{\frac{-g\cos\theta}{R}}. Hence the minimum \omega is \sqrt{\frac{-g\cos\theta}{R}}.

Is this correct?

 

[haruspex]

Hence the minimum \omega is \sqrt{\frac{-g\cos\theta}{R}}.

Is this correct?

For part 5, it says 'for any theta', so you need an answer independent of theta.
But there's an error in part 4. Check your algebra. I think you'll find there's a sign wrong in the given answer. As it happens, it does not affect part 5.

 

[lemaitre]

For part 5, it says 'for any theta', so you need an answer independent of theta.
But there's an error in part 4. Check your algebra. I think you'll find there's a sign wrong in the given answer. As it happens, it does not affect part 5.

Hi haruspex. Thank you for pointing that out. I have corrected it. Did I do Question 3 correctly?

Also, I'd appreciate it if you give me more hint for Question 5. Does it have anything to do with conservation of energy?

By the way, I should have mentioned, this is not a homework question. I'm working on a past exam paper for an upcoming exam.

 

[haruspex]

I'd appreciate it if you give me more hint for Question 5.

You need an ω such that $\omega^2 ≥ \frac{-g\cos\theta}{R}$ for all θ. Clearly that's true whenever cos θ is positive. What is the max value that ω² has to beat?