Maximum and minimum speeds in a moving cube

[Jenny Physics]

Homework Statement

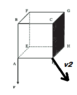
A rigid cube in the figure moves in space. At a certain time $t$ its front face $ABCD$ is vertical and the velocity of vertex $A$ is vertical down $v$ while the velocity of its vertex $D$ makes an angle with the vertical and has magnitude $v_{2}$ while lying on the plane of the front face. Assume that the speed of vertex $H$ is $v_{3}$ and lies on the plane of the black face at that instant. Assume that the side of the cube is $s$.

(a) Can you write $v_{3}$ in terms of $v$ and $v_{2}$ at time $t$?

(b) What are the points in the cube that have the minimum and maximum velocity at time $t$?

Homework Equations

Rigid cube motion.

The Attempt at a Solution

[/B]
Not sure. It must have something to do with translations and rotations of a rigid cube/square but not sure how to approach this problem.

 

[haruspex]

not sure how to approach this problem.

A useful first step could be to find a different reference frame that simplifies things a little.
Then consider how an adjacent vertex (of those mentioned) might be moving. Create variables as necessary to represent that.

But.. seems to me there is not enough info for the first part.

 

[Charles Link]

I think I sort of know how to work this problem. The motion of the cube involves a motion of its center at some velocity $\vec{v}_o$ plus a rotation that passes through its center of angular velocity vector $\vec{\omega}$. The velocity $\vec{v}$ of any point $\vec{r}$ from the center can be written as $\vec{v}=\vec{v}_o+\vec{\omega} \times \vec{r}$. With that, you might be able to come up with a closed form answer for the velocity at the vertex $H$. $\\$ And like @haruspex , I'm not sure whether there is sufficient info for a complete answer. That remains to be determined.

 

[Jenny Physics]

A useful first step could be to find a different reference frame that simplifies things a little.
Then consider how an adjacent vertex (of those mentioned) might be moving. Create variables as necessary to represent that.

But.. seems to me there is not enough info for the first part.

I imagine I could pick a reference frame at one of the vertices, say $A$. This is the origin of the reference frame. Then I can define axes $x,y,z$, say $z$ is from $A$ to $D$, $x$ is from $A$ to $E$ and $y$ is from $A$ to $B$. In this frame, vertex $D$ would have velocity $v\hat{y}-v_{2y}\hat{y}+v_{2x}\hat{x}$ while $H$ would have velocity $v\hat{y}+v_{3x}\hat{x}+v_{3y}\hat{y}$...

 

[haruspex]

I could pick a reference frame at one of the vertices, say A.

Right, but I was thinking of such a frame moving with A.

Edit: please define your x, y, z directions.

 

[Jenny Physics]

Suppose you know exactly how the line AH moves. That must satisfy all the given info about the motions of A and H, but leaves a degree of freedom for D.

The velocity of $D$ and $H$ lie in the specified planes. Maybe this restricts the freedom?

 

[haruspex]

The velocity of $D$ and $H$ lie in the specified planes. Maybe this restricts the freedom?

Which planes? I see none specified, but there are some implied.

 

[Jenny Physics]

Which planes? I see none specified, but there are some implied.

The velocity of $D$ lies on the front face plane, and the velocity of $H$ lies on the black face plane.

 

[haruspex]

The velocity of $D$ lies on the front face plane, and the velocity of $H$ lies on the black face plane.

Yes, you are right about H - I missed that (because it said "speed" but should say velocity). But D is not restricted to the front face plane. You cannot tell which plane the arrow is in.

Edit: however, I still see a difficulty. Even if we know exactly how A and D move, within the given constraints, I can see a degree of freedom for the movement of H.

 

[Delta2]

I think I sort of know how to work this problem. The motion of the cube involves a motion of its center at some velocity $\vec{v}_o$ plus a rotation that passes through its center of angular velocity vector $\vec{\omega}$. The velocity $\vec{v}$ of any point $\vec{r}$ from the center can be written as $\vec{v}=\vec{v}_o+\vec{\omega} \times \vec{r}$. With that, you might be able to come up with a closed form answer for the velocity at the vertex $H$. $\\$ And like @haruspex , I'm not sure whether there is sufficient info for a complete answer. That remains to be determined.

The system of equations seems to be just completely determined (neither overdetermined or underdetermined). We have two unknown vectors $\vec{v}_0$ and $\vec{\omega}$, and two vector equations that we get if we apply $\vec{v}=\vec{v}_o+\vec{\omega} \times \vec{r}$ for $\vec{r}=\vec{r_A}$ and $\vec{r}=\vec{r_D}$. Totally we have 6 algebraic equations and 6 unknowns, the x,y,z components of the vectors $\vec{v_0}$ and $\vec{\omega}$.
@haruspex Given what I said just above, how do you see a degree of freedom for the movement of H?

The only thing which is abit free for me, is if the centre of rotation coincides with the centre of the cube. If it does not then the system of equations is underdetermined as we also have as unknown the center of rotation $\vec{r_0}$, we would have 3 unknown vectors and 2 vector equations in this case.

 

[haruspex]

how do you see a degree of freedom for the movement of H?

E.g. A and D moving straight down same speed. The cube can rotate at arbitrary rate around AD.

 

[Delta2]

E.g. A and D moving straight down same speed. The cube can rotate at arbitrary rate around AD.

That could be the case, and then the centre of rotation is not the c.o.m of the cube.

In the absence of external forces a rigid body can rotate only around its c.o.m, but of course the way the problem is given does not imply that we don't have forces acting on the cube.

 

[haruspex]

That could be the case, and then the centre of rotation is not the c.o.m of the cube.

In the absence of external forces a rigid body can rotate only around its c.o.m, but of course the way the problem is given does not imply that we don't have forces acting on the cube.

Yes, I had not interpreted it as implying it is a massive body with no external forces. It is not even clear that the cube has mass - it is just a shape. But that may be what needs to be assumed.

 

[haruspex]

we have 6 algebraic equations

We do not. We only know the magnitude of D's velocity and one constraint on the direction of H. That leaves us one equation short.

 

[Delta2]

We do not. We only know the magnitude of D's velocity and one constraint on the direction of H. That leaves us one equation short.

My bad, I didn't read carefully the statement, and because $v_2$ (as well as $v$) was drawn in the scheme I thought we knew everything about it.

 

[Charles Link]

Yes, you are right about H - I missed that (because it said "speed" but should say velocity). But D is not restricted to the front face plane. You cannot tell which plane the arrow is in.

Edit: however, I still see a difficulty. Even if we know exactly how A and D move, within the given constraints, I can see a degree of freedom for the movement of H.

I think it does say the velocity vector of $D$ lies in the plane of the front face. Thereby it seems they may have given enough info for a solution.

 

[Charles Link]

Additional item is that I think the earlier discussion was mixing kinematics with dynamics. The center of mass should be of no concern here. To specify the motion of a rigid body, 6 parameters are needed. $\\$ I think any point $P$ of the rigid body can be taken as the point of reference, and the motion can be described by the velocity vector $\vec{v}_p$ of that point, along with an angular velocity vector $\vec{\omega}_p$ for a rotation with axis through the point $P$, and $\vec{\omega}_p$ will depend on the point $P$ that was chosen. $\\$ [Edit comment: I believe the required rotation $R$ and thereby the resulting $\vec{\omega}$ will, in fact, be independent of the point $P$ that is selected]. $\\$ e.g. If the body undergoes a movement of some kind from its initial location, you can displace a point $P$ in the body to its new location $\vec{r}'_p$, and then perform a rotation of some kind with point $P$ remaining stationary, and that will locate the body exactly where it needs to be. $\\$ In this case, one choice for the point $P$ is the center of the cube, but it is not necessary to pick that point as the point $P$. It might simplify things to use the vertex $A$ as the point $P$.

 

[Charles Link]

I know as a homework helper, I'm not supposed to supply answers, but this case is a little different, as it seems to have a couple of us scratching our heads. If the velocity vector $\vec{v}$ of vertex $A$ were zero, I think we could conclude that $\vec{v}_2=\vec{v}_3$ [Edit note: See post 20=we later concluded this is not necessarily the case], and I think that is also the case if $\vec{v}$ is non-zero. $\\$ Did I reach an incorrect conclusion, or is this problem quite simple once the right point ($A$) is chosen as the reference? $\\$ Edit: My next question is, how can $\vec{v}_2$ possibly point in any direction but vertical? If we rotate about the axis through $A$ with the axis of rotation perpendicular to the front face, the vector $\vec{v}_2$ necessarily points in the vertical direction. (Because $\vec{v}_2$ lies in the plane of the front face, the rotation we do using vertex $A$ as a reference must have its axis perpendicular to the front face).

 

[Jenny Physics]

I know as a homework helper, I'm not supposed to supply answers, but this case is a little different, as it seems to have a couple of us scratching our heads. If the velocity vector $\vec{v}$ of vertex $A$ were zero, I think we could conclude that $\vec{v}_2=\vec{v}_3$, and I think that is also the case if $\vec{v}$ is non-zero. $\\$ Did I reach an incorrect conclusion, or is this problem quite simple once the right point ($A$) is chosen as the reference? $\\$ Edit: My next question is, how can $\vec{v}_2$ possibly point in any direction but vertical? If we rotate about the axis through $A$ with the axis of rotation perpendicular to the front face, the vector $\vec{v}_2$ necessarily points in the vertical direction. (Because $\vec{v}_2$ lies in the plane of the front face, the rotation we do using vertex $A$ as a reference must have its axis perpendicular to the front face).

Why would $v_{3}=v_{2}$? What rule is being used to find velocities at any point of the dark face?

 

[Charles Link]

Let's write out the vector equations: Let's assume for simplicity that point $A$ has zero velocity.$\\$ (Edit: The case where $\vec{v}_A \neq 0$ will just require a simple addition to the following results. We will work in the rest frame of $A$. I could have then used primes $\vec{v}_2'$ and $\vec{v}_3'$ on the velocity vectors, but the concepts should be clear in any case). $\\$ We have $\vec{v_2}=v_{2i}\hat{i}+v_{2j} \hat{j}=\vec{\omega}_A \times s \hat{i}$. That means $\vec{\omega}_A$ has no $\hat{j}$ component, or $\vec{v}_2$ would get a non-zero $\vec{k}$ component. It does not rule out a component in the $\hat{i}$ direction for $\vec{\omega}_A$. $\\$ In any case $v_{2i}$ is necessarily zero, because the $s \vec{i}$ is the $\vec{r}$ in the $\vec{\omega} \times \vec{r}$ term. ($\vec{v}_2$ must be perpendicular to $s \hat{i}$ ). $\\$ It appears the $\hat{i}$ component of $\vec{\omega}_A$ remains undetermined. Because the location of $H$ is $\vec{r}_H= s \hat{i}-s \hat{k}$, any non-zero $\hat{i}$ component of $\vec{\omega}_A$ will result in a non-zero $v_{3j } \hat{j}$ component for point $H$ that gets added to the $v_{3j}$ from the $\omega_{Ak} \hat{k}$ rotation. .$\\$ (This term is $\omega_{Ai} \, s \hat{j}$ and it will add to the $v_{3j} \hat{j}$ from the $\omega_{Ak} \hat{k}$ rotation which results in a $\omega_{A k} \hat{k} \times s \hat{i}=\omega_{Ak} \, s \hat{j}$ term). $\\$ From this it would appear there is insufficient info to compute $\vec{v}_3$, and in addition, my statement in post 18 that $\vec{v}_2=\vec{v}_3$ would appear to be incorrect. It could be the case, but it doesn't have to be.

 

[Charles Link]

A follow-on to the previous post: Note if $\vec{\omega}_A$ has only a $\hat{k}$ component, then $\vec{v}_2=\vec{v}_3$. $\\$ If $\vec{\omega}_A$ has a non-zero $\hat{i}$ component, then $\vec{v}_2 \neq \vec{v}_3$.