Wxfsa
- 22
- 0
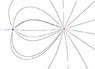
Homework Statement
http://i.imgur.com/haX3OW8.png
Homework Equations
The Attempt at a Solution
I guess a) is 1/3 (probably wrong, because I assumed all the field lines that end at -q originates at +3q which is not necessarily true) but I can't figure out b)