- #1
Karol
- 1,380
- 22
Homework Statement
Homework Equations
First derivative=maxima/minima/vertical tangent/rising/falling
The Attempt at a Solution
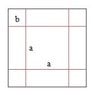
a are the sides of the base and b is the height
$$A=4ab+a^2,~~V=a^2b=a^2\frac{A-a^2}{4a}=...=\frac{1}{4}a(A-a^2)$$
$$V'=\frac{1}{4}(A-a^2-2a^2)=\frac{1}{4}(A-3a^2)$$
$$V'=0~\rightarrow~a=\sqrt{\frac{A}{3}},~b=\frac{\sqrt{3A}}{4}$$
According to the book b should be ##~\displaystyle \frac{1}{2}\sqrt{A/3}##