nvrslep303
- 6
- 0
A 3.07-kg object is thrown vertically upward from the surface of Earth, where the acceleration due to gravity is g1 = 9.81m/s2. The intial velocity is v1, and the object reaches a maximum height of y1. What is the maximum height, y2, if the object is thrown at a speed of v2 = 1.15v1 from the surface of Saturn's moon Rhea? The acceleration due to gravity on Rhea is g2 = 0.264 m/s2. Give your answer as a multiple of y1.
Relevant equations
I tried using the equation
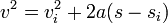
I used the equation and got
0 = v2 + 19.62h and
0 = 1.15v2 + .528h
but I'm not sure what to do next. the answer is supposed to be like this:
y2 = ____ x y1
but I'm not too sure on where to go from where I'm at. Any hints? It would be greatly appreciated
Relevant equations
I tried using the equation
The Attempt at a Solution
I used the equation and got
0 = v2 + 19.62h and
0 = 1.15v2 + .528h
but I'm not sure what to do next. the answer is supposed to be like this:
y2 = ____ x y1
but I'm not too sure on where to go from where I'm at. Any hints? It would be greatly appreciated