IamNotAPhysicist
- 1
- 0
Homework Statement
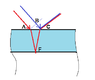
A transparent film( n = 1.45) is placed on a glass surface( n = 1.14) and is illuminated by light ( incidence angle α = 60°. What is the minimum thickness d1 of film such that reflection of light with λ is minimized, while if the thickness is d2 then with the same λ the reflection is maximized?
Homework Equations
2dcosβ = (m - .5)λ/n
β = 36.6°
m = 0,1,2,3...
d - film thickness
λ = light wavelength in vacuum (air)
The Attempt at a Solution
I am not good at physics, but I am supposed to do my homework. So, I pointed out that I am dealing with constructive interference and found the equation I showed above(used "Physics for Scientists and Engineers" A.Serway for that).
My first problem is to find λ. I tried to substitute d2 in the equation and then I understood that I don't know what value of m I should use. For example, I used m = 1 and got λ = 648×10^(-9). But in this case, how am I supposed to find d1? If I use the same equaton, the same m and λ I will get d1 = d2. I've got completely confused by these maximum and minimum reflections