Maximum normal stress and shear stress

[Moara]

Homework Statement

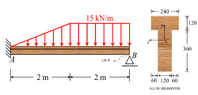
A cantilever with elasticy modulus ($E = 13 \ GPa$) is subjected to the distribution of forces as in figure. The cross section T shaped is indicated in the figure. The moment of inertia with respect to the centroidal axis $z$ is $1496.45 \cdot 10^6 \cdot mm^4$. In the absence of the distribution of forces, there is a lack of $0.5 mm$ between the bean and the mobile support. Knowing that the bean touches the support with the load distribution, find:
1) The maximum normal stress
2) The value of the maximum shear stress in the body
3) The deflection in the middle of the bean

Relevant Equations

$\sum{F_y} = 0$, $\sum{M} = 0$

First, I am trying to find the external reactions in A and B, but I have only one equation relating $V_A$ and $V_B$, what other relation could I use ?
Once I find the reactions, I can find the external moment as well. Then, I may draw the diagram of moments in each cross section and then find the maximum Moment. Using that $\sigma = -My/I$ I can find the maximum normal stress.

 

[Moara]

Indeed, maybe we can try to find the general formula for the displacement of the beam and then impose that $v(4) = -0.5 mm$. With that, I think we may find $V_A, V_B, M_A$ and find the diagram of moments, to find its maximum value

 

[Chestermiller]

What would the end deflection be if B was not there?