Maximum power transfer theorem leading to erroneous result Why?

[Barloud]

Hi everybody,

Below is a circuit that I am investigating. All the components are linear, nothing fancy here.

My goal is to maximize the average power P dissipated in the resistor Re. To this aim, I am only allowed to play with the angular frequency ω of the voltage source and with the value of the resistor Re. All the other parameters are set to fixed values.

First approach: from Kirschoff's law, I derive an expression for the average power P dissipated in Re. I have then to solve simultaneously dP/dRe=0 and dP/dω=0 in terms of Re and ω. The second equation does however correspond to a high order polynomial in ω (7th I think I remember) for which analytical solutions are not known.

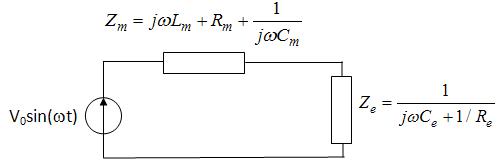
Second approach: I transform the initial circuit into the Thevenin equivalent shown below. I then apply the maximum power transfer theorem stating that maximum power will be dissipated in Ze when Ze=Zm*. If some conditions on the parameters other than Re and ω are fulfilled, I obtain two couples of solution in Re and ω respecting Ze=Zm*. And here comes my problem: while these couple of solutions respect dP/dRe=0 from the first approach, they are not solutions of dP/dω=0.

While one may suggest an error in the derivations, I checked it many times with symbolic computations software. I rather believe that the maximum power transfer theorem does not yield in the particular situation that I consider, but I do not manage in finding the reason, neither from a mathematical or physical point of view. Any help would be appreciated.

 

[Philip Wood]

The maximum power theorem deals gives the optimum load impedance (Z_e) for a given power supply impedance (Z_m).

I don't think it applies here, because, by allowing ω to alter, you no longer have a given (i.e. constant) Z_m. You alter both Z_e and Z_m at the same time.