Maxwell-Boltzmann Distribution Alpha and Beta

[kidsasd987]

Hi, I have a question about Maxwell-Boltzmann Distribution.

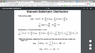
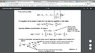
First, because of mass conservataion and energy conservatioin, Sum Ni and Sum EiNi must be constant.
Partial of both sum will be 0.

Is that why we adopted constant alpha as a parametric constant? because without alpha, partial Nj of Sum Ni will be 1 and there must be inequality because partial Nj of Sum Ni has to be 0. And would that mean alpha and beta will be always 0?

 

[MisterX]

If you are trying to extremize some function $S(N_1, N_2, \dots, N_n)$ with respect to some constraint $f(N_1, N_2, \dots, N_n)=0$ it must be that at the extreme point the tangent space of the level set of $S$ coincides with the tangent of the constraint level set. Otherwise you could make a differential change to the $N_i$ in a direction allowed by the constraint and obtain a different value of $S$. Thus $S$ would not be extremized.

The statement that the level sets have the same tangent space is the same as saying the gradients of $S$ and $f$ must be proportional to one another. We call these proportionality constants Lagrange multipliers.

In the above example there are two constraints instead of one. The constants $\alpha$ and $\beta$ are the Lagrange multipliers. $\alpha$ and $\beta$ will not always be 0.