Me In What My Teacher Said Is Easy

  • Thread starter Thread starter Chikawakajones
  • Start date Start date
  • Tags Tags
    Teacher
AI Thread Summary
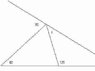
To find the value of x in the triangle problem, it is essential to apply the theorem that states the measure of an external angle equals the sum of the two opposite angles. Given that one of the opposite angles is 50 degrees, the angle adjacent to the external angle of 125 degrees can be calculated as 180 - 125. The next step involves using the supplementary angle property, where the sum of two angles on a straight line equals 180 degrees. Ultimately, the calculations lead to determining the value of x through geometric reasoning rather than specific formulas. Understanding these principles is crucial for solving the problem effectively.
Chikawakajones
Messages
22
Reaction score
0
Find the value of x. Show all work with justifications.
 

Attachments

  • Credit.jpg
    Credit.jpg
    3 KB · Views: 465
Physics news on Phys.org
The sum of the three angles in a triangle is 180 degrees. The sum of two angles making a line is also 180 degrees: that leads to the well known theorem (it's probably in your text) that the measure of an external angle (here the one marked "125") is equal to the sum of the measures of the two opposite angles. One of those two opposite angles is 50 degrees. From that you can find the measure of the angle between "80" and "x" and then find x.
 
Are there any "formulas" to find "x" in this particular problem?...
 
Not that I know of
 
Chikawakajones said:
Are there any "formulas" to find "x" in this particular problem?...

Beside this one
A+B+C=180°
,where A,B,C are the three angles of a plane triangle,nope.
But,as Ivy said,u need to know that the sum of two supplementary angles is 180°.

This is all u need to know to get it done.

Daniel.
 
Again there are no formulas to solve this problem, it is all geometrical.

Step one.
Look at the angle 125. 180-125 will give you the angle on the other side of the line.

Step two add 55+50 and minus the product from 180. this is the upper angle.

Step three add 80+75 then minus that from 180 and that is the angle x
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Loop equations for this battery-resistor circuit
Replies
48
Views
2K
How Does a Teacher of Science Differ from a Science Teacher?
Replies
2
Views
518
Secondary Teacher
Replies
3
Views
372
Newbie Introduction
Replies
4
Views
852
Who Misinterpreted the Motion Equation, Me or My Teacher?
Replies
4
Views
2K
What are some challenges faced by first year science teachers in rural areas?
Replies
2
Views
357
Balmer series experiment
Replies
2
Views
919
How to calculate the wind speeds produced by an ionic thruster
Replies
7
Views
907
Finding path difference of EM waves received by radio telecopes
Replies
3
Views
1K
Shout out to my HS Science teacher from 10 years ago
Replies
2
Views
947

Hot Threads

Recent Insights

Back
Top