- #1
Athraxin
- 20
- 2
Hi people,
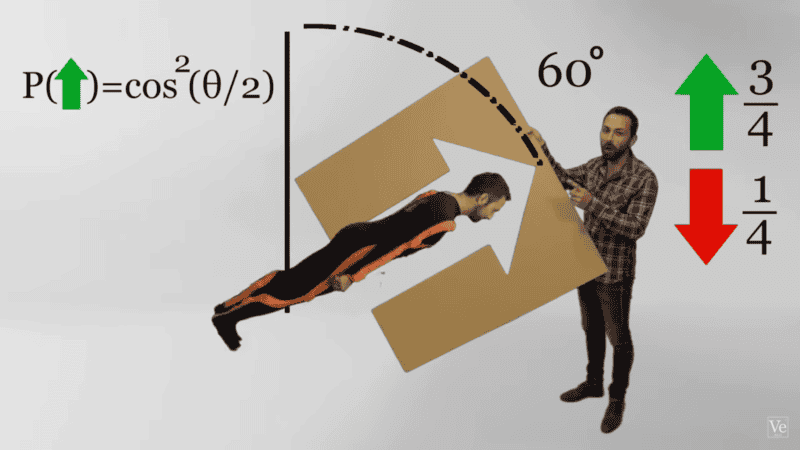
Lets assume, we have a stern gerlach setup and we are going to measure an atom's last orbit electron's spin with 60 degree from vertical axis. Therefore, in this case, our outcomes would be 3/4 for spin up, 1/4 for spin down.
Let's assume, we have the same setup but we are going to measure the spin of the last orbital electron of one of the entangled atoms with the same axis. In this case what would be the results for this action?
Entangled state:
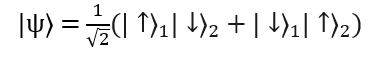
Would it change the results or wouldn't it?

[1] - Veritasium.
Lets assume, we have a stern gerlach setup and we are going to measure an atom's last orbit electron's spin with 60 degree from vertical axis. Therefore, in this case, our outcomes would be 3/4 for spin up, 1/4 for spin down.
Let's assume, we have the same setup but we are going to measure the spin of the last orbital electron of one of the entangled atoms with the same axis. In this case what would be the results for this action?
Entangled state:
Would it change the results or wouldn't it?
[1] - Veritasium.
Last edited: