Mechanical engineering Swing of Death

[gl0ck]

Hi there,
again maybe stupid question but I have no idea about this exercise.
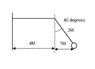
or maybe a little clue. i know that v=r?
but with the given 40° when i convert it to a rmp it is very small value 0.111111
and the r is 3m or 7m..
Please if someone can help me..
also if someone can help me with the FBD of A wheel being hauled up a slope by a wire attached to its axle.

 

[CWatters]

You should show your working before asking for help.

and the r is 3m or 7m.

For example how did you arrive at two values? Neither match the answer I got.

 

[gl0ck]

I just wondered if the r is equal to the wire attached or the whole body of the swing?
that is how i find 3m and 7m because the string is 3m long and the whole body is 7m

 

[CWatters]

Neither.

With the wire hanging down vertically the radius would be 4m. With the ride spinning around at very high speed the wires would fly out and up until almost horizontal and the radius would be approx 4 + 3=7.

However the problem asks what speed is necessary for them to be at a 40 degree angle to the vertical. You can use basic trig to work out the exact radius. It's 4M + ?M in the diagram...

 

[CWatters]

Re your PM. Best I reply on thread so anyone else with similar question sees the follow up..

Thanks for the replies on both of the topics.
i)So the high should be 3*(1-cos40) = 3*(1-0.766) = 0.7019? and the total radius should be 4.7019?

No the radius would be..

= 4M + ?M see my diagram.
= 4 + 3Sin(40)
= 4 + 1.93
= 5.93m

To find the speed of rotation in RPM v=r*? but how to find the ? ?
ii)also the tension must be equal to mg/cos40?
iii)still don't have any idea

Since it's not moving vertically the vertical components must sum to zero.

Lets take downwards as +ve

-T*cos(40) + m*g = 0
so
T = m*g/cos(40).........(Eq 1)

Now for the horizontal..

In order for it to move in a circle the wire must provide centripetal force = mv²/r towards the centre so..

T*sin(40) = m*v²/r
T = m*v²/(r*sin(40)) ......(Eq 2)

over to you