NAkid
- 70
- 0
[SOLVED] mechanical waves
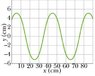
A sinusoidal transverse wave is traveling along a string in the negative direction of an x-axis. The figure shows a plot of the displacement as a function of position at time t=0; the y-intercept is 4.0m. The string tension is 6.8N, and its linear density is 47.22 g/m.
Find the amplitude (cm).
Find the wavelength (cm).
Find the wave speed (cm/s).
Find the period of the wave.
Find the maximum transverse speed of a particle in the string.
What is the phase angle in degrees?
So linear density is the mass per unit length. it's not in the units we want (kg/cm), so convert and get 4.722E-4 kg/cm.
wave speed = sqrt(T/wave length) = sqrt(6.8/4.722E-4), but this isn't the right answer. did i convert wrong?
also I'm having trouble finding the amplitude and wave length, probably for the same reason as above.
Homework Statement
A sinusoidal transverse wave is traveling along a string in the negative direction of an x-axis. The figure shows a plot of the displacement as a function of position at time t=0; the y-intercept is 4.0m. The string tension is 6.8N, and its linear density is 47.22 g/m.
Find the amplitude (cm).
Find the wavelength (cm).
Find the wave speed (cm/s).
Find the period of the wave.
Find the maximum transverse speed of a particle in the string.
What is the phase angle in degrees?
Homework Equations
The Attempt at a Solution
So linear density is the mass per unit length. it's not in the units we want (kg/cm), so convert and get 4.722E-4 kg/cm.
wave speed = sqrt(T/wave length) = sqrt(6.8/4.722E-4), but this isn't the right answer. did i convert wrong?
also I'm having trouble finding the amplitude and wave length, probably for the same reason as above.