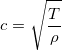Waves on a String -- Minimizing reflections from the far end (ring on a bar)

[Loubrainz]

Homework Statement

A string of linear density ρ terminates in a small ring of mass m. A horizontal bar is passed through the ring, perpendicular to the direction of the string at rest, and the string is stretched to a tension T. Friction between the ring and the bar generates a resistive force –bv_y, where v_y is the transverse velocity of the ring and b is a constant. A harmonic wave of angular frequency ω is directed along the string towards the ring. To what value of T should the string be stretched to minimise the energy flux in the reflected wave, and what is the energy reflection coefficient at this tension? (Assume that ω m/b <<1).

Homework Equations

F = ma (Newton's Second Law)
y(x,t)_i = Ae^i(ωt-kx) (mathematical description of incident wave)
y(x,t)_r = Be^i(ωt+kx) (mathematical description of reflected wave)

(wave equation)

(wave speed in terms of tension and linear density)

(Power passing through a point on a string with some amplitude 'a')
Energy Reflection Coefficient = Reflected Energy/Incident Energy

The Attempt at a Solution

My initial thoughts are, firstly, that there is a geometrical boundary condition: the displacement of the incident and reflected wave at the ring must be continuous:
y_i(x=0) = y_r(x=0) (letting the position of the ring be at x=0);
therefore, A=B. (?)

Secondly, the net transverse force acting on the ring must be the combined transverse components of the tension in the string from both the incident and reflected wave balanced by the friction between the ring and rod:

I tried substituting in the mathematical description of the incident and reflected wave, but it doesn't seem to rearrange into anything immediately useful that can be plugged into the power equation.

What do you think?

 

[Orodruin]

My initial thoughts are, firstly, that there is a geometrical boundary condition: the displacement of the incident and reflected wave at the ring must be continuous:
yi(x=0) = yr(x=0) (letting the position of the ring be at x=0);
therefore, A=B. (?)

This is not correct. The amplitudes can only be the same if the wave is completely reflected. You need to get the boundary condition from the force balance on the ring instead.

I suggest that you instead write the full wave as $y(x,t) = A e^{i(\omega t - kx)} + B e^{i(\omega t + kx)}$, where $A$ is the amplitude of the incoming and $B$ the amplitude of the reflected wave. Also note that you can express the resistive force in terms of the wave function $y(x,t)$ and its derivatives at $x = 0$.

Also note that you can normalise the incoming wave amplitude to one.