[Mechanics] Calculate the braking torque

[hugo_faurand]

Homework Statement

We have a wheel spinning with a speed of 20rad/s.
The brake exerts a tangential force of 2073.6N and a normal force of 5760N.
(No radius given for the wheel)

1/Calculate the braking torque exerted by the braking force.

2/ Calculate how much rotations the wheel do before it stops

(3/ Which scaleswould be interesting to calculate ?)

Relevant Equations

Inertia of the wheel : 100m²/kg
μ=0.36

Hello ev

eryone !

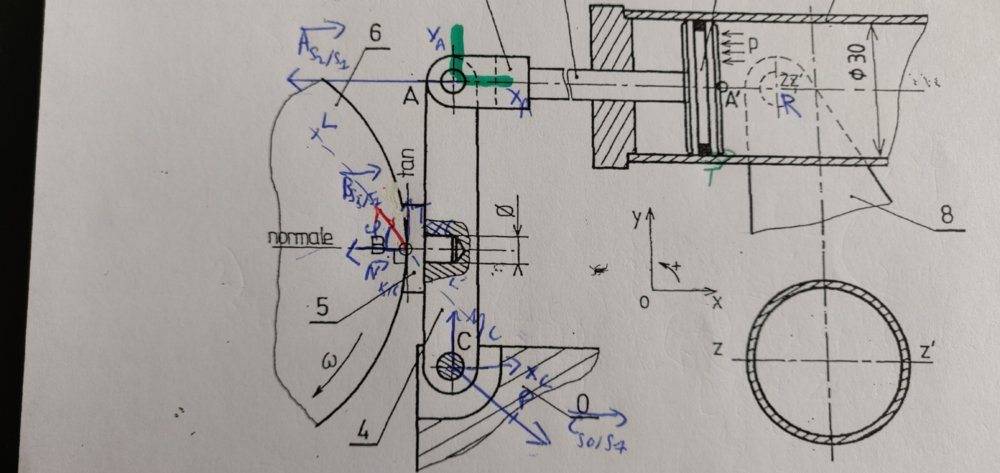
I've got a problem in engineering class with a braking system (picture linked).
In the first part I calculated the friction force $$ \vec{B} $$ with components :
T (following y axis) : 2073.6N
N (following x axis) : 5760N.

For the first question I struggle a lot because I haven't seen dynamics equations yet.
But on the web I saw that we can calculate the braking torque C with the equation :
$$C= J \times \alpha $$ alpha is the rotational acceleration. But our wheel is spinning at a constant speed so $$\alpha=0$$ and thus C=0 and that's strange. I found another formula : $$C= n \times N \times \mu \times r $$ r stands for the radius of the wheel, n is the number of pair of frictionning surfaces here 1 and N the normal force acting on the wheel.

This one is interesting because although we don't have the radius (I think that's an error from my teacher) we'll have a non-zero value.

For the question 2/ I use the kinetic energy theorem that tells us that the work of the system is equal to the difference of kinetic energies. So we have $$W = \frac{1}{2} J \omega_2^2 - \frac{1}{2} J \omega_1^2 = \frac{1}{2} J (\omega_2^2-\omega_1^2)$$
Whereas $$W=J\times \theta $$ thus we have $$ \theta = \frac{W}{C} $$

Here is one solution for me and then we just have to divide the result by 2 pi to have the number of laps.

For the last question I've got no idea maybe the power...

So if you can help me because I'm not really sure of my work.
For the radius of the wheel maybe I can just take an arbitrary value, if the literal steps are good I think that's the most important.

Thx in advance

 

[FactChecker]

One comment:
I think that the rotational speed is an initial speed, not a constant speed, as you state ($\alpha =0$). I say that because part of the problem is to determine when the wheel stops.

 

[hugo_faurand]

One comment:
I think that the rotational speed is an initial speed, not a constant speed, as you state ($\alpha =0$). I say that because part of the problem is to determine when the wheel stops.

That's right but we have no statement about the duration of the braking. So we can't determine the deceleration.

 

[BvU]

we can calculate the braking torque $C$ with the equation :$$C=J\times\alpha$$

Conversely, if we know $C$, we can calculate the deceleration rate !

(assume you are right about '(I think that's an error from my teacher) ' and use the symbol $r$ )

 

[hugo_faurand]

I made all the calculations with a radius of 53mm and I've a torque of almost 39 N.m and it needs 4laps to stop. Is it coherent ?

(Otherwise spend good end of the year festivities !)