Ahmed Ayman
- 11
- 3
Member advised to use the formatting template for all homework help requests
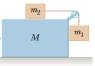
Can anyone please explain to me how can I calculate the "Tension" and "acceleration" of M in this question interms of M,m1,m2 and g?
I can't understand how M has an acceleration or why M is involved in the calculation of the tension
my solution was that acc of M is zero
and Tension = m1g x (m2/(m2+m1))
Thanks in advance

I can't understand how M has an acceleration or why M is involved in the calculation of the tension
my solution was that acc of M is zero
and Tension = m1g x (m2/(m2+m1))
Thanks in advance

Attachments
Last edited: