Mesh Analysis for time domains?

[jisbon]

Homework Statement

Solve the following mesh circuit.

Relevant Equations

-

I've tried to solve the following circuit using mesh equation, but the solution seems to differ from my attempted answer.

Mesh circuit as follows:

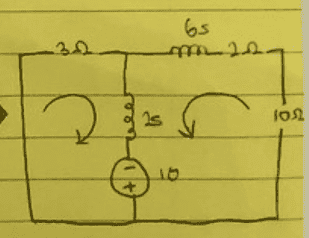
My mesh equation is:

-10+3(i1)+2s(i1-i2)=0 (for the mesh on the left)
and
-10+12(i2)+6s(i2)+2s(i2-i1)=0 (right mesh)

However the answer seems to be different and claims that the equation are as follows:

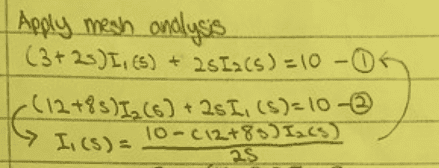
Am I missing something here?
Thanks

 

[Delta2]

You have to show us how you took the directions of currents $I_1,I_2$ to be

And why you say in time domain since it seems you doing it in the s-domain (Laplace transformed currents)?

 

[jisbon]

Sorry, what I meant was s domain.
As shown in the diagram, I1 is in the clockwise direction, while I2 (the one on the right) is in anticlockwise.

 

[Delta2]

Then in your equations you should put $I_1+I_2$ where you have $I_1-I_2$ (or $I_2-I_1$) and then your answer is the same with the book answer.
You should put $I_1+I_2$ because that's what we get -given the current directions as you say -if we apply KCL at the junction with the 3$\Omega$ resistor the 6s coil and the 2s coil ,

 

[Delta2]

Sorry I now understood you use mesh currents, but still the total mesh current in the branch that has the source and the 2s coil is $I_1+I_2$ because one is clockwise and the other counterclockwise.

 

[jisbon]

Sorry I now understood you use mesh currents, but still the total mesh current in the branch that has the source and the 2s coil is $I_1+I_2$ because one is clockwise and the other counterclockwise.

Oh I see. So if they are in the same direction, my old equations will then be correct?
This:
10+3(i1)+2s(i1-i2)=0 (for the mesh on the left)
and
-10+12(i2)+6s(i2)+2s(i2-i1)=0 (right mesh)

 

[Delta2]

Oh I see. So if they are in the same direction, my old equations will then be correct?
This:
10+3(i1)+2s(i1-i2)=0 (for the mesh on the left)
and
-10+12(i2)+6s(i2)+2s(i2-i1)=0 (right mesh)

Yes I believe the above equations are correct if both are anticlockwise.

 

[Joshy]

I agree with Delta. You draw both of the currents in the same direction and so their sign should not flip.