Eveflutter
- 14
- 0
Member warned that the homework template is required
When using the method of differences on a given series, when do you stop listing the terms?
Example question:
f(r)=
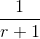 ; r∈N
; r∈N
State f(r)-f(r+1) in terms of r and hence determine
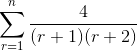
So skipping until the worked answer gives
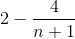
Great so here I included the n+1th term because I'm guessing since the larger number in the given: f(r)-f(r+1) was r+1 so that's why I stop here? I'm not sure.
Okay so that guess works for that one but what about this one:
Example question (2):
Given f(r)= r(r+1)! show that f(r)-f(r-1)= r!(r2 +1) and hence solve
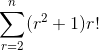
Alright skipping the proof once again and going into the expansion part, I have this thus far:
(3!2 - 2!1) + (4!3 - 3!2) + (5!4 + 4!3) + ... + (here is where I'm not sure what to stop at)
Possibilities:
stopping with the subbing of the nth term ... + ((n-1)n! - (n-1)!(n-2)) + (n(n+1)! - n!(n-1))
or stopping with the subbing of the (n+1)th term ... + ((n+1)!n - n!(n-1)) + ((n+2)(n+1)! - (n+1)!n)
The respective answers I may end up with are:
at nth term: n(n+1)! - 2
at (n+1)th term: (n+1)(n+1)! - 2
Any help will be appreciated ^3^ Thank you~!
Example question:
f(r)=
State f(r)-f(r+1) in terms of r and hence determine
So skipping until the worked answer gives
Great so here I included the n+1th term because I'm guessing since the larger number in the given: f(r)-f(r+1) was r+1 so that's why I stop here? I'm not sure.
Okay so that guess works for that one but what about this one:
Example question (2):
Given f(r)= r(r+1)! show that f(r)-f(r-1)= r!(r2 +1) and hence solve
Alright skipping the proof once again and going into the expansion part, I have this thus far:
(3!2 - 2!1) + (4!3 - 3!2) + (5!4 + 4!3) + ... + (here is where I'm not sure what to stop at)
Possibilities:
stopping with the subbing of the nth term ... + ((n-1)n! - (n-1)!(n-2)) + (n(n+1)! - n!(n-1))
or stopping with the subbing of the (n+1)th term ... + ((n+1)!n - n!(n-1)) + ((n+2)(n+1)! - (n+1)!n)
The respective answers I may end up with are:
at nth term: n(n+1)! - 2
at (n+1)th term: (n+1)(n+1)! - 2
Any help will be appreciated ^3^ Thank you~!