hubrisos
- 3
- 0
- Homework Statement
- A conducting sphere of radius a is made up of 3 different shells, upper part a/2 \leq z \leq -a/2, the middle part -a/2 \leq z\leq a, the lower part -a \leq z \leq -a/2 where the center of the sphere is at the origin. The upper part V and the lower part has -V potentials, while the mid part is grounded. Find the electric potential at x up to a 4 T order in the expansion of a/x << 1.
Basically the shell has 3 regions, upper, middle, lower. the lower/upper parts are not hemispherical, middle part is relatively broad, and the upper part has V, the lower part has -V potential.
- Relevant Equations
- green functions
A conducting sphere of radius a is made up of 3 different shells, upper part a/2
 z
z
 -a/2, the middle part -a/2
-a/2, the middle part -a/2
 z
z
 a, the lower part -a
a, the lower part -a
 z
z
 -a/2 where the center of the sphere is at the origin. The upper part V and the lower part has -V potentials, while the mid part is grounded. Find the electric potential at x up to
-a/2 where the center of the sphere is at the origin. The upper part V and the lower part has -V potentials, while the mid part is grounded. Find the electric potential at x up to
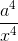 order in the expansion of a/x << 1.
order in the expansion of a/x << 1.
Basically the shell has 3 regions, upper, middle, lower. the lower/upper parts are not hemispherical, middle part is relatively broad, and the upper part has V, the lower part has -V potential.
I don't know where to start, I don't ask you to solve the entire thing, but give me a few tips/hints. I am lost due to the fact that the mid part is huge.
Basically the shell has 3 regions, upper, middle, lower. the lower/upper parts are not hemispherical, middle part is relatively broad, and the upper part has V, the lower part has -V potential.
I don't know where to start, I don't ask you to solve the entire thing, but give me a few tips/hints. I am lost due to the fact that the mid part is huge.