^_^physicist
- 231
- 1
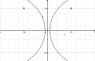
I've been working with image charges for a while now, and I have noticed that I haven't been able to find a single discussion on the use of image charges for concave geometries (i.e. a charge on the "inside" of a catenary shaped curved conducting plate, see attached picture). Has anyone worked with a problems of this nature before? Anyone know of any resources that discuss problems of this nature? I have been racking my brain for a over a few days and I can't seem to figure out how to a approach a problem like this. I almost just broken down and tried to solve these geometries with boundary conditions and the laplace/possion equations (depending on the problem), but they become a mess way to quickly.
Any help is appreciated.
(A note on the picture, the point on the right is a negative charge and the point on the right is a positive charge. I am very concerned with this problem for a research project; however, I would be just as happy (in fact more so) if someone could give an explanation for solving the simplified problem of just looking at the left-hand side (or right-hand side) of the graph)
Any help is appreciated.
(A note on the picture, the point on the right is a negative charge and the point on the right is a positive charge. I am very concerned with this problem for a research project; however, I would be just as happy (in fact more so) if someone could give an explanation for solving the simplified problem of just looking at the left-hand side (or right-hand side) of the graph)