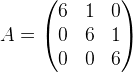Discussion Overview
The discussion revolves around calculating the matrix power $$A^{17}$$ for a specific matrix structure, exploring patterns and properties of matrix powers, particularly in the context of upper triangular matrices and Jordan blocks. The conversation includes theoretical considerations and mathematical reasoning.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
Main Points Raised
- One participant notes that in the matrix $$A^{17}$$, the entries where there are 6's will be $$6^{17}$$, while expressing uncertainty about the pattern in the right side of the triangle, suggesting the left will be zero.
- Another participant suggests that the Cayley-Hamilton theorem might be useful for the calculation.
- A later post presents a specific form of the matrix and calculates $$A^{17}$$, indicating it results in an upper triangular matrix with specific entries involving powers of $$a$$ and coefficients related to the position in the matrix.
- Further exploration discusses the general form of a Jordan block and how to express its powers using the binomial theorem, detailing the nilpotent structure and its implications for the matrix powers.
Areas of Agreement / Disagreement
Participants express various approaches and calculations regarding the matrix power, but there is no consensus on a single method or result. Multiple competing views and methods remain present in the discussion.
Contextual Notes
The discussion includes assumptions about the structure of the matrix and the properties of nilpotent matrices, but these assumptions are not universally agreed upon or fully explored.
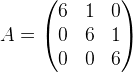 .
.