- #1
Goodver
- 102
- 1
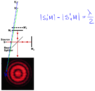
Since 2 splitted beams meet at ONE spot later on, we have just one beam which flows to the detector, therefore I expect to see just one light spot, where the BRIGHTNESS is changing depending on at which phase 2 beams meet. Pattern with fringes happens when we have multiple sources, like Young's experiment or difraction grating.
why we have fringes here if there is only one source?
why we have fringes here if there is only one source?