Minimal force to turn over a tube

[Karol]

Homework Statement

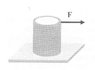
The tube weighs 100[kg], is 1.2[m] high with radius 0.4[m] and is on a rough surface. a force is applied at the top. the first question was what's the magnitude to turn over the tube, but the second was what's the minimal force needed to do that.

Homework Equations

Moment: M=FxR

The Attempt at a Solution

I don't understand the second question since it's already in the best position and direction for that.
The answer in the book for the minimal force is 272[N]

 

[gneill]

Perhaps consider other locations and directions to apply the force? How might you maximize the moment that results from the applied force?

 

[Karol]

I found, thanks