Minimizing the area of a channel in contact with water

[Zouatine]

Homework Statement

Hi everybody,
I found some difficulty to understand the following exercise and that solution,
Statement of Exercise:
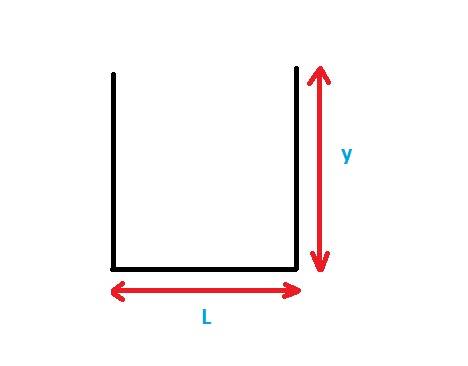
Either a uniform rectangular channel of slope (i),
What are:the draft (height) (y),and the width (L) for the wet section to be minimal.

Relevant Equations

Aw= Area of channel= y*L,
Pw= Perimeter wet =y+2L,

My problem:
In the solution,our teacher found, that the wet section is minimal if y=L/2
So
Am: = L^2 /2;
Pm: = 2L;
So despite that I try with any value, I can not find a more minimal section,
and that's not the case because if I try with y = L / 3 I find
Am: L^2/3;
Pm: (5/3)*L ;
and these values are less than the value of y = L / 2.
so why that ? is that because I did not understand the exercise or our teacher made a mistake?

Thank you

 

[haruspex]

Pw= Perimeter wet =y+2L,

because I did not understand the exercise

Quite so. You are looking for the minimum of 2y+L (not y+2L) for a given area A.
The y=L/2 solution gives L=√(2A), P=√(8A).
Your y=L/3 gives L=√(3A),;P=√(25A/3).
25/3>8.